La quantità di moto, definita come il prodotto della massa di un corpo per la sua velocità, è una grandezza vettoriale fondamentale per descrivere lo stato dinamico di un sistema. Il suo principio di conservazione assume un’importanza strategica nell’analisi dei sistemi fisici, poiché permette di risolvere problemi complessi, come urti ed esplosioni, senza la necessità di conoscere i dettagli delle forze interne scambiate. Questo principio non è un postulato a sé stante, ma deriva direttamente dalle leggi fondamentali della dinamica di Newton; rappresenta, di fatto, una prospettiva più fondamentale sul Terzo Principio quando applicato a sistemi chiusi, riformulando il concetto di “azione-reazione” in termini di scambio di quantità di moto.
Il teorema dell’impulso
Il teorema dell’impulso stabilisce un legame quantitativo diretto tra una forza applicata a un corpo per un determinato intervallo di tempo e la conseguente variazione della sua quantità di moto. Questo teorema è di fondamentale importanza pratica, specialmente nell’analisi di fenomeni impulsivi come urti, collisioni o percussioni, dove forze di grande intensità agiscono per intervalli di tempo molto brevi.
La derivazione del teorema è una diretta conseguenza algebrica del Secondo Principio della Dinamica. Partendo dalla formulazione F = ma e considerando l’accelerazione media a = Δv/Δt, si procede come segue: F = m(Δv/Δt). Moltiplicando entrambi i membri per Δt e riconoscendo che mΔv è la variazione della quantità di moto Δq (per massa costante), si ottiene la relazione finale:
F Δt = Δq
Questa equazione è nota come teorema dell’impulso.
La grandezza fisica al primo membro dell’equazione, data dal prodotto della forza per l’intervallo di tempo in cui essa agisce, è definita come impulso (I).
I = F Δt
L’impulso è una grandezza vettoriale con la stessa direzione e lo stesso verso della forza che lo ha generato.
Nel Sistema Internazionale (SI), l’impulso si misura in newton · secondo (N·s). Questa unità è dimensionalmente equivalente a quella della quantità di moto (kg·m/s): 1 N·s = 1 (kg·m/s²) · s = 1 kg·m/s.
Il teorema dell’impulso può essere interpretato in due modi complementari, entrambi di grande utilità fisica:
- da sinistra a destra (
I→Δq): un impulso I applicato a un corpo provoca una variazione della sua quantità di moto Δq esattamente pari all’impulso stesso; - da destra a sinistra (
Δq→F): una variazione di quantità di moto Δq che avviene in un intervallo di tempo Δt molto breve implica la presenza di una forza impulsiva F di intensità molto elevata.
Quest’ultima interpretazione è cruciale per comprendere come eventi apparentemente semplici possano generare forze di entità straordinaria.
Esempio pratico
Per illustrare la potenza esplicativa del teorema dell’impulso, analizziamo il caso di un martello che colpisce un chiodo. Il fattore chiave è la brevissima durata dell’impatto (Δt), che amplifica la variazione di quantità di moto del martello in una forza impulsiva di enorme intensità.
I dati del problema sono i seguenti:
- massa del martello (
m): 1.5 kg; - variazione di velocità (
Δv): da 15 m/s a 0 m/s (quindi |Δv| = 15 m/s); - intervallo di tempo (
Δt): 0.02 s; - area della punta del chiodo (
A): 0.5 mm² (pari a 0.5 · 10⁻⁶ m²).
Calcolo della Forza Impulsiva (F)
Utilizzando il teorema dell’impulso nella forma F = |Δq| / Δt = m|Δv| / Δt, si calcola la forza media esercitata dal martello:
F = (1.5 kg · 15 m/s) / 0.02 s = 1.125 N
Questa forza, pari al peso di un oggetto di circa 115 kg, è generata da un martello di soli 1.5 kg.
Calcolo della Pressione (p)
Questa forza viene trasmessa alla punta del chiodo. Data la sua area estremamente ridotta, la pressione (p = F/A) esercitata sul materiale è immensa:
p = 1.125 N / (0.5 · 10⁻⁶ m²) = 2.25 · 10⁹ Pa
Tale pressione, equivalente a circa 22.500 atmosfere, spiega perché un chiodo possa penetrare materiali resistenti. Questo esempio dimostra come il teorema quantifichi le forze e le pressioni eccezionali generate durante eventi impulsivi.
Dall’analisi della dinamica di un singolo corpo, è naturale passare a considerare come la descrizione del moto dipenda dall’osservatore, introducendo così il concetto di relatività del moto.
Il principio di relatività galileiana
La descrizione del moto di un oggetto è intrinsecamente legata al sistema di riferimento scelto. Un ruolo speciale è ricoperto dai sistemi di riferimento inerziali, definiti come quei sistemi in cui vale il primo principio della dinamica. In tali sistemi, un corpo non soggetto a forze nette si muove di moto rettilineo uniforme. Il principio di relatività galileiana postula che le leggi della fisica assumono la stessa forma matematica in tutti i sistemi di riferimento inerziali. Ciò significa che nessun esperimento di meccanica può distinguere uno stato di quiete da uno di moto rettilineo uniforme.
Per correlare le misure di velocità effettuate da due osservatori in moto relativo rettilineo uniforme, si utilizzano le trasformazioni galileiane. Se un osservatore misura una velocità va e un secondo osservatore si muove rispetto al primo con una velocità relativa costante vb, la velocità v misurata dal primo osservatore è data dalla composizione vettoriale dei moti:
v(t) = va(t) + vb(t)
Esempio pratico
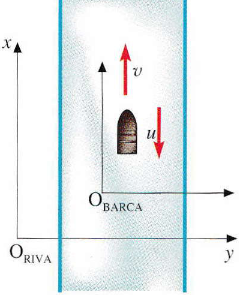
Consideriamo una barca che si muove in un canale con corrente.
Definiamo le seguenti velocità: v è la velocità intrinseca della barca rispetto all’acqua, u è la velocità della corrente rispetto alla riva, e ud è la velocità della barca (che naviga controcorrente) misurata dalla riva.
- Osservatore sulla riva (
ORIVA): questo osservatore misura la velocità della barca rispetto al proprio sistema di riferimento, ud, e la velocità dell’acqua, u. Per determinare la velocità propria della barca, applica la legge di composizione delle velocità ud = v + u. Risolvendo per v, ricava la velocità intrinseca della barca: v = ud – u. - Osservatore sull’acqua (
OACQUA): questo osservatore si muove solidale con la corrente. Dal suo punto di vista, la velocità della barca è direttamente v. Egli può verificare la coerenza delle osservazioni misurando la velocità della riva, che gli appare muoversi a –u, e la velocità della barca rispetto alla riva, ud.
La conclusione fondamentale è che entrambi gli osservatori, applicando correttamente le trasformazioni galileiane ai propri dati sperimentali, determinano lo stesso identico valore per la grandezza fisica v, la velocità della barca rispetto all’acqua. Ciò convalida il principio di relatività, dimostrando che le leggi del moto sono coerenti in tutti i sistemi di riferimento inerziali.
Dominio di validità e limiti del principio
Le trasformazioni galileiane sono estremamente accurate per le velocità incontrate nell’esperienza quotidiana e in gran parte delle applicazioni ingegneristiche. Tuttavia, il loro dominio di validità è limitato a velocità molto inferiori a quella della luce nel vuoto (c ≈ 3 · 10⁸ m/s).
L’evidenza sperimentale ha dimostrato che la velocità della luce è una costante universale. Secondo la relatività galileiana, se una sorgente in moto con velocità v emettesse un raggio di luce, un osservatore a terra si aspetterebbe di misurarne la velocità come c + v. Gli esperimenti, invece, mostrano che la velocità misurata è sempre c, indipendentemente da v. Questo risultato sperimentale, che contraddice la semplice addizione vettoriale galileiana, può essere riassunto simbolicamente con l’espressione v ⊕ c = c, dove ⊕ rappresenta la composizione relativistica delle velocità. Questa incongruenza ha segnato il limite della meccanica classica e ha spianato la strada alla Teoria della Relatività Ristretta di Einstein.
Fonte: Fisica biomedica.