L’analisi dei sistemi fisici, dalle dinamiche molecolari ai grandi complessi meccanici, non può prescindere da una comprensione rigorosa dei meccanismi di trasferimento energetico. Il lavoro e l’energia non devono essere intesi come meri costrutti algebrici, ma come il linguaggio universale che descrive l’evoluzione dello stato di un sistema e la reversibilità dei processi naturali.
Il concetto di lavoro e le sue dimensioni fisiche
Nella meccanica classica, il lavoro rappresenta il meccanismo fondamentale di trasferimento di energia tra sistemi. Una forza compie lavoro nel momento in cui il suo punto di applicazione subisce uno spostamento, agendo come un operatore che modifica l’energia del corpo su cui agisce.
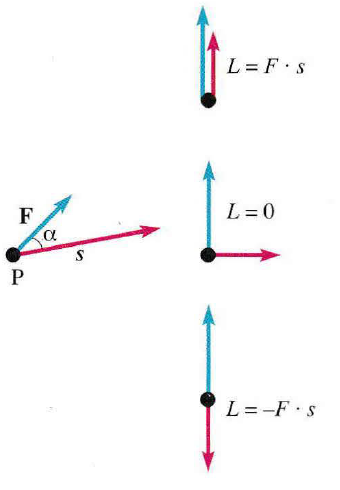
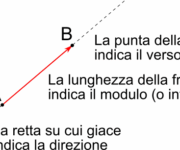
Consideriamo una forza costante F applicata a un punto materiale che subisce uno spostamento rettilineo s. Il lavoro L è definito analiticamente come il prodotto scalare tra i vettori forza e spostamento:
L’angolo α tra i due vettori determina la natura del trasferimento:
- lavoro motore: per
0 ≤ α < π/2, il lavoro è positivo; la forza ha una componente concorde al moto e incrementa l’energia del sistema; - lavoro resistente: per
π/2 < α ≤ π, il lavoro è negativo; la forza si oppone allo spostamento (come nel caso dell’attrito); - lavoro nullo: per
α=π/2, la forza è ortogonale allo spostamento e non compie lavoro. Come illustrato nell’immagine, una forza può essere intensa ma risultare nulla ai fini del bilancio energetico se la sua direzione non incide sulla traiettoria.
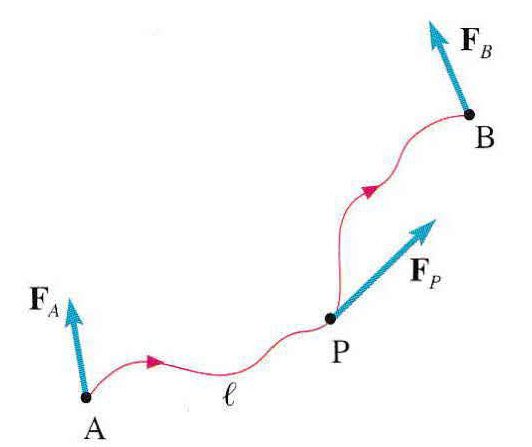
In contesti reali, dove la forza varia nello spazio o la traiettoria ℓ è complessa, il lavoro è calcolato come l’integrale di linea lungo il cammino da A a B:
Questa formulazione scompone il percorso in infiniti tratti infinitesimi d𝐬 lungo i quali la forza può essere considerata localmente costante, garantendo un rigore analitico assoluto anche per campi di forza non uniformi.
Sistemi di misura e rigore metrico
Un’analisi scientifica richiede un quadro metrico standardizzato. Il Joule è l’unità fondamentale nel Sistema Internazionale, ma il fisico deve saper operare tra diverse scale di grandezza.
| Sistema di misura | Unità di misura | Fattore di conversione |
|---|---|---|
| S.I. (Internazionale) | Joule (J) | 1 N m |
| C.G.S. | erg | 1 J = 107 erg |
| Pratico | Chilogrammetro (kgm) | 1 J = 1/9.806 kgm (1 kgm ≈ 9.8 J) |
| Scala atomica | Elettronvolt (eV) | 1 J = 1,602176565 × 10⁻¹⁹ |
Perché privilegiare il lavoro rispetto alle leggi di Newton? Mentre l’approccio newtoniano è intrinsecamente vettoriale e richiede la conoscenza dettagliata di ogni forza istantanea, il metodo energetico, basato su una grandezza scalare, permette di determinare lo stato finale di un sistema (es. la velocità) senza dover risolvere le equazioni differenziali del moto lungo l’intero percorso. È questa astrazione che conferisce al calcolo energetico una potenza risolutiva superiore nei sistemi complessi.
Energia cinetica
Caricamento…
Il trasferimento di energia mediante lavoro si manifesta macroscopicamente come variazione dello stato di moto, definendo quella che chiamiamo energia cinetica.
Un corpo di massa m in moto con velocità v possiede una capacità di compiere lavoro definita come:
Il legame tra dinamica e lavoro discende direttamente dal secondo principio di Newton. Per un moto rettilineo uniformemente accelerato, lo spazio percorso s in un tempo Δt è dato dal prodotto tra la velocità media vm=1/2(v1+v2) e il tempo stesso. Sostituendo a=(v2−v1)/Δt nella formula del lavoro:
Otteniamo così il teorema dell’energia cinetica:
Per un corpo che parte da fermo sotto l’azione di una forza costante, la velocità finale è semplicemente
Tuttavia, se operiamo in presenza di forze dissipative (attriti), il lavoro totale è la somma del lavoro motore e del lavoro resistente. In questo caso, ΔEk sarà inferiore al lavoro motore erogato, poiché una frazione dell’energia viene degradata in calore.
Campi di forze e l’origine dell’energia potenziale
La distinzione tra forze conservative e dissipative rappresenta la linea di demarcazione tra processi meccanici reversibili e degradativi.
Una forza è conservativa se il lavoro compiuto su una traiettoria chiusa è nullo:
In termini fenomenologici, il lavoro tra due punti A e B è indipendente dal cammino. Al contrario, le forze di attrito sono sempre dirette in senso opposto al moto; il loro lavoro è costantemente negativo e non si annulla mai su un percorso chiuso, portando alla variazione di energia cinetica anche in cicli completi (ΔEk≠0).
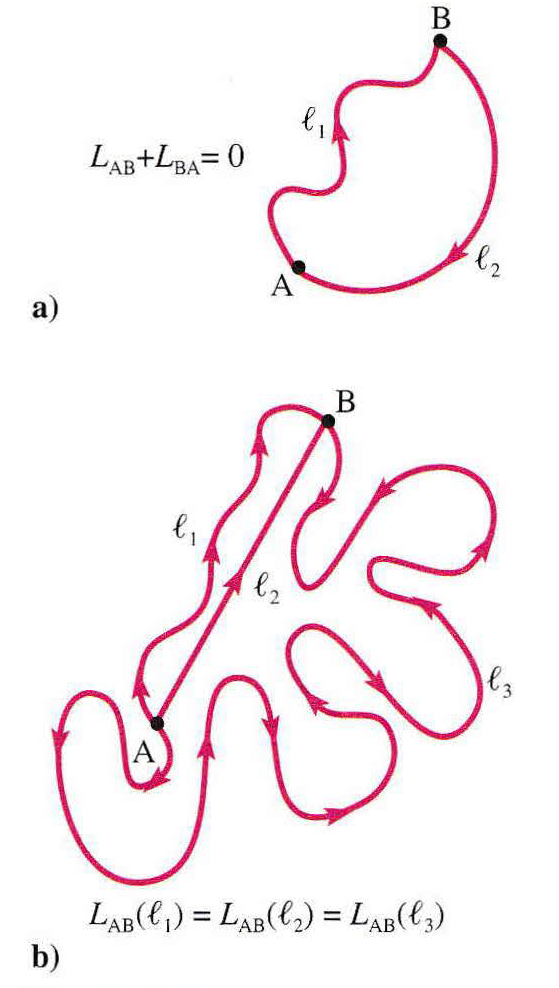
L’indipendenza dal cammino permette di introdurre una funzione delle coordinate spaziali denominata energia potenziale U(x,y,z), tale che:
Questa funzione caratterizza completamente il campo: conoscere U significa conoscere l’intera capacità del campo di generare forza e compiere lavoro. Tra i campi conservativi fondamentali ricordiamo:
- campi radiali: dove la forza varia in maniera inversamente proporzionale al quadrato della distanza (es. gravitazione universale, elettrostatica);
- campi uniformi: forza costante in ogni punto (es. gravità in prossimità del suolo);
- campi elastici: caratterizzati da una forza di richiamo proporzionale allo spostamento.
Teorema di conservazione dell’energia meccanica
In un sistema isolato soggetto esclusivamente a forze conservative, la somma dell’energia cinetica e potenziale rimane costante: Ek+U=costante.
Nel caso del campo gravitazionale U=mgh+cost, la costante dipende dalla quota di riferimento (solitamente h=0 al suolo).
Nel campo elastico l’energia accumulata in una molla compressa o tesa di un tratto x è
Esempi
Il salto con l’asta
Un atleta di élite raggiunge una velocità di circa 10 m/s (limite biologico umano). Trasformando l’energia cinetica in potenziale gravitazionale
si ottiene un incremento di quota h ≈ 5.1 m. Considerando che il centro di gravità iniziale si trova già a circa 1 m dal suolo, l’altezza totale raggiunta è 6.1 m, valore coerente con i record mondiali di circa 6.2 m.
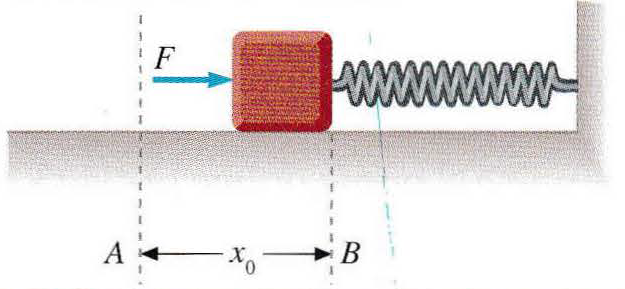
Compressione elastica
Un corpo che urta una molla trasforma la propria energia cinetica in energia potenziale elastica. La compressione massima si ottiene dall’uguaglianza:
Fonte: Fisica biomedica.