Come fa la Terra ad attrarre una mela che cade da un albero, o la Luna in orbita, senza toccarle direttamente? Questa domanda, apparentemente semplice, ci porta a uno dei concetti più potenti della fisica: l’idea che un oggetto possa modificare lo spazio che lo circonda. Per descrivere questa “azione a distanza”, i fisici hanno sviluppato il modello del campo di forze. Questo strumento concettuale ci permette di immaginare lo spazio non come un vuoto passivo, ma come un’entità attiva, pervasa da influenze invisibili.
Per comprendere a fondo come la gravità modelli il nostro universo, dobbiamo prima definire con precisione cosa intendiamo per campo di forze, quali sono le sue proprietà e come possiamo visualizzarlo.
Un campo di forze è una proprietà dello spazio. Più precisamente, possiamo definirlo come una regione in cui, per ogni singolo punto, è possibile determinare la forza che agirebbe su un corpo se fosse posizionato lì. Matematicamente, questa relazione è espressa come:
F = F(x, y, z)
In termini semplici, un campo di forze è come una mappa tridimensionale. Invece di indicare città o montagne, questa mappa assegna a ogni punto dello spazio un vettore forza, ovvero un’informazione precisa su intensità e direzione della forza in quel punto.
Dato che un campo è invisibile, i fisici usano uno strumento grafico per rappresentarlo: le linee di forza. Queste linee ci forniscono un’immagine intuitiva della struttura del campo e seguono due regole fondamentali:
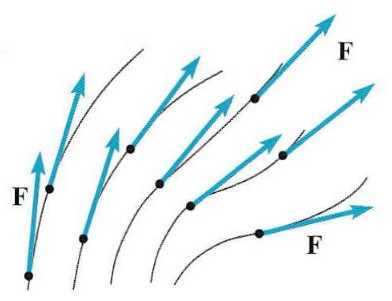
direzione: in ogni punto, il vettore forza F è sempre tangente alla linea di forza che passa per quel punto. Questo significa che la linea di forza indica, istante per istante, la direzione della forza applicata a un corpo;
visualizzazione: le linee di forza offrono una rappresentazione visiva immediata della “forma” e della direzione del campo nello spazio.
Cosa succede se ci sono più sorgenti a generare un campo, ad esempio due pianeti vicini? In questo caso, vale il principio di sovrapposizione lineare dei campi. L’idea centrale è molto semplice: la forza totale che agisce su un oggetto in un punto è la somma vettoriale delle singole forze che ogni sorgente, da sola, eserciterebbe in quel punto.
Il Campo Gravitazionale Terrestre
Il campo gravitazionale è l’esempio perfetto per vedere in azione le idee di campo e linee di forza. La sua descrizione, tuttavia, cambia in modo significativo a seconda della scala di osservazione che adottiamo: una cosa è descrivere l’attrazione su un satellite, un’altra è descriverla su una penna che cade dalla scrivania.
Per descrivere la forza di gravità su larga scala, ad esempio tra pianeti o tra la Terra e la Luna, utilizziamo la Legge di Gravitazione Universale formulata da Newton.
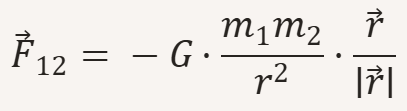
Analizziamo i termini chiave di questa equazione fondamentale:
Forze di attrazione gravitazionale tra due masse. Per il terzo principio della dinamica F12 = -F21
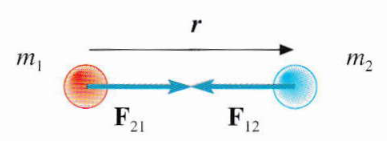
m1 e m2: sono le due masse che si attraggono reciprocamente;
r: è la distanza tra i centri delle due masse.
G: è la costante di gravitazione universale (6.67 * 10-11 N * m2/kg2). Il suo valore estremamente piccolo ci dice che la gravità è una forza intrinsecamente debole, che diventa significativa solo in presenza di masse enormi (come quelle dei corpi celesti);
il segno meno (-): indica che la forza è sempre attrattiva, ovvero ogni massa attira l’altra verso di sé;
(r / |r|): questo termine è un vettore unitario (un vettore di lunghezza 1) che ha la stessa direzione del vettore r che congiunge le due masse. La sua funzione è unicamente quella di dare una direzione alla forza (lungo la linea che unisce le masse) senza alterarne l’intensità.
Su questa scala globale, le linee di forza del campo gravitazionale terrestre sono radiali: puntano tutte direttamente verso il centro della Terra, come i raggi di una ruota.
Quando consideriamo un oggetto vicino alla superficie terrestre (ad esempio, all’interno di una stanza), la situazione si semplifica enormemente. L’approssimazione chiave è che la distanza r dal centro della Terra può essere considerata costante e pari al raggio terrestre R.
Partendo dalla legge universale F = G * (MTerra * m) / r2, e applicando l’approssimazione che r è quasi uguale al raggio terrestre R, otteniamo F ≈ G * (MTerra * m) / R2. Possiamo raggruppare tutti i termini costanti in un’unica grandezza, che chiamiamo g:
g = G * MTerra / R2
In questo modo, la forza di gravità locale, che chiamiamo Forza Peso (P), si semplifica nella nota formula:
P = m * g
In questa equazione, g è l’accelerazione di gravità e il suo valore standard è 9.81 m/s2. In questa visione locale, le linee di forza sono considerate praticamente parallele tra loro e perpendicolari al suolo. Di conseguenza, il campo gravitazionale in una regione limitata (come un laboratorio) viene definito uniforme: la forza mg è la stessa in ogni punto.
È importante notare che questo valore è una media; nella realtà, g varia leggermente sulla superficie terrestre a seconda della latitudine e dell’altitudine.
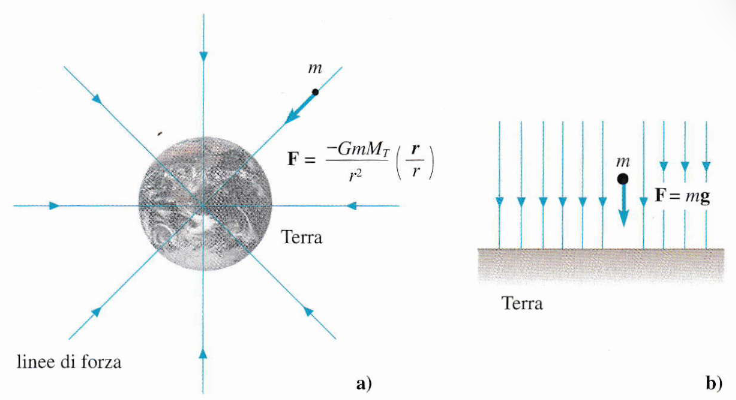
Linee di forza del campo gravitazionale: (a) a grande distanza dalla Terra, il campo è radiale; (b) vicino alla superficie terrestre, il campo è uniforme con g=9,81 m/s2
Per consolidare la comprensione, la seguente tabella mette a diretto confronto le differenze chiave tra la descrizione globale e quella locale del campo gravitazionale terrestre.
Caratteristica
Visione a grande distanza (generale)
Visione locale (vicino alla superficie)
Legge della forza
Usa la formula di Newton: F = -G * (M*m / r2)
Usa la formula della forza peso: P = m*g
Dipendenza dalla distanza
La forza diminuisce con il quadrato della distanza (1/r2)
La forza è considerata costante (non dipende dall’altezza)
Per caratterizzare un campo in modo che non dipenda dall’oggetto usato per “sentirlo”, si introduce il concetto di intensità del campo. L’intensità è definita come la forza che agisce sulla massa unitaria (cioè su 1 kg di massa).
Il vantaggio di questa grandezza è che descrive una proprietà intrinseca dello spazio, indipendente dalla “massa sonda” che usiamo per misurarla. Nel caso del campo gravitazionale, il vettore che rappresenta l’intensità del campo è proprio l’accelerazione di gravità g.
