Nel caratterizzare una grandezza fisica attraverso la sua misura, non sempre è sufficiente indicare un unico numero che rappresenti il rapporto tra la grandezza data e l’unità di misura scelta come riferimento.
Ad esempio, consideriamo la velocità. Dire che un oggetto si muove a 50 km/h non fornisce un’informazione completa, poiché manca l’indicazione della direzione e del verso del movimento. Allo stesso modo, se si dicesse a una persona di spostarsi di 3 metri, non sarebbe chiaro dove andare, in quanto non sono state specificate né una direzione né un verso.
Per descrivere completamente alcune grandezze fisiche, è quindi necessario ricorrere a strumenti matematici più complessi dei semplici numeri. In questo contesto, introduciamo il concetto di quantità vettoriali. È importante tenere presente che questo concetto può essere ulteriormente esteso a entità matematiche ancora più complesse, dette tensori. I tensori trovano ampio impiego nelle teorie fisiche avanzate. Un esempio è il tensore di Riemann, che descrive la geometria dello spazio-tempo e che è caratterizzato da ben 16 numeri.
Possiamo dunque distinguere due tipologie fondamentali di grandezze fisiche:
grandezze scalari: sono quelle che, una volta stabilita l’unità di misura, sono completamente definite da un numero. Esempi di grandezze scalari sono volume, massa, energia;
grandezze vettoriali: per definirle è necessario specificare, oltre al numero (detto modulo del vettore), anche una direzione e un verso. Esempi di grandezze vettoriali sono spostamento, velocità, accelerazione, forza, e così via.
A questo punto, si pone il problema di come rappresentare matematicamente le grandezze vettoriali.
Una rappresentazione intuitiva ed efficace è quella geometrica: consiste nel rappresentare un vettore come un segmento orientato, la cui:
direzione e verso corrispondono a quelli della grandezza vettoriale;
lunghezza è proporzionale al modulo del vettore, cioè all’intensità della grandezza stessa.
Rappresentazione geometrica di un vettore mediante un segmento orientato.
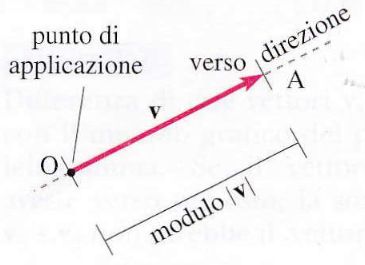
In alcuni casi, può essere necessario specificare anche il punto di applicazione del vettore. Dal punto di vista simbolico:
una grandezza vettoriale viene indicata con una lettera in grassetto, ad esempio v;
il modulo del vettore può essere indicato semplicemente come v oppure come |v|.
Tuttavia, la rappresentazione geometrica presenta uno svantaggio: richiede una manipolazione grafica, che può risultare poco pratica nel caso si vogliano eseguire operazioni tra vettori. Per questo motivo, è utile introdurre una seconda rappresentazione matematica, che permetta di trasformare il calcolo vettoriale in un calcolo numerico tra grandezze scalari.
Questa seconda modalità di rappresentazione si basa sul concetto di proiezione di un vettore in un sistema di riferimento.
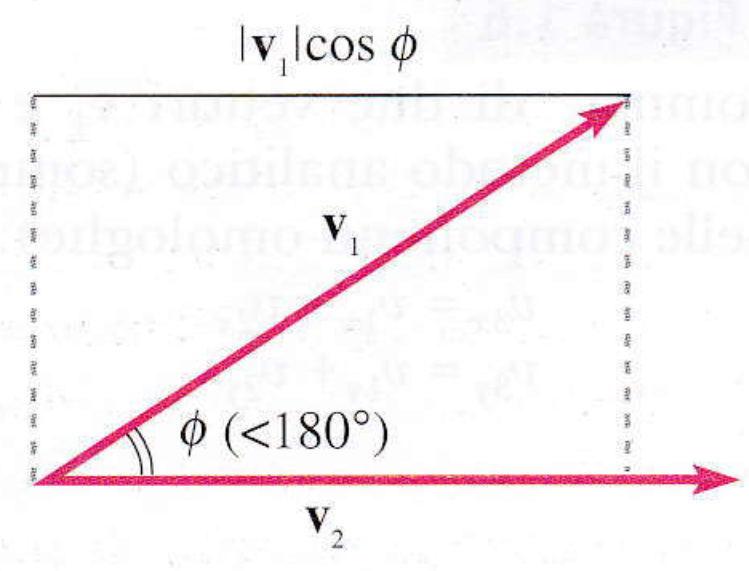
Ad esempio, dato un vettore v = ĀŌ e una direzione individuata da una retta r, che forma un angolo ϕ con v, si definisce componente del vettore v nella direzione r la quantità:
vr=v⋅cosϕ
Proiezione del vettore v sulla retta r: vr rappresenta la componente del vettore v lungo la direzione r.
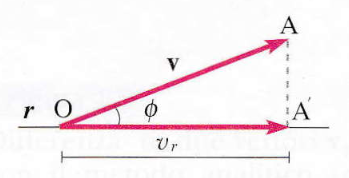
Questa misura la lunghezza del segmento ottenuto proiettando v sulla retta r (vedi l’immagine accanto).
Il vettore componente del vettore v lungo la retta r è rappresentato dal vettore Ā’Ō.
In generale, un vettore v può essere scomposto lungo due o più direzioni, ottenendo i vettori componenti corrispondenti a ciascuna di esse.
Possiamo ora utilizzare il concetto di componente (o proiezione) di un vettore per mostrare che un vettore può essere rappresentato mediante tre numeri e un sistema di riferimento.
Rappresentazione di un vettore mediante le tre componenti in un sistema di riferimento cartesiano ortogonale.
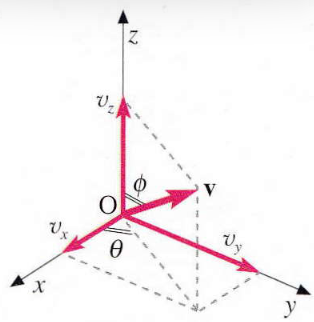
Un sistema di riferimento si ottiene, ad esempio, definendo tre rette orientate uscenti dallo stesso punto origine. Se queste tre rette sono mutuamente perpendicolari, si parla di sistema cartesiano ortogonale, i cui assi vengono solitamente indicati con le lettere x, y e z.
Dato un vettore v e un sistema di riferimento cartesiano, possiamo determinarne le tre componenti lungo gli assi. Indichiamo queste componenti con vₓ, vᵧ e vz. Il vettore v può quindi essere rappresentato da:
tre numeri: le sue componenti lungo gli assi;
il sistema di riferimento in cui tali componenti sono state calcolate.
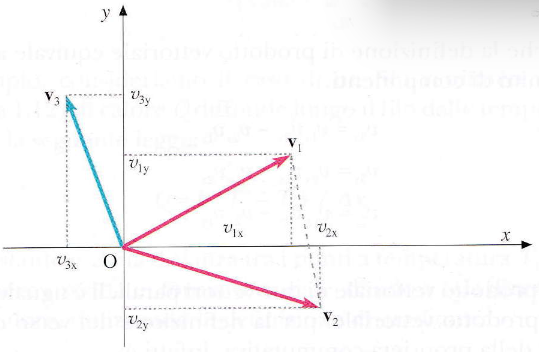
Riferendoci all’immagine accanto, le componenti del vettore v si esprimono come:
Da queste componenti, il modulo del vettore può essere calcolato con la relazione:
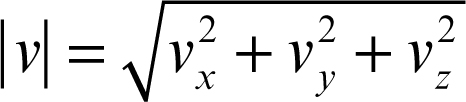
È fondamentale comprendere che, mentre le componenti del vettore dipendono dal sistema di riferimento, il vettore stesso è indipendente da esso. Infatti, immaginando il vettore come un segmento orientato nello spazio, è evidente che cambiando il sistema di riferimento cambiano le sue componenti, ma non il vettore in sé.
Somma e differenza di vettori
Consideriamo due vettori v₁ e v₂ aventi lo stesso punto di applicazione (origine). Se i vettori inizialmente non condividono la stessa origine, uno di essi (o entrambi) può essere traslato parallelamente a sé stesso fino a far coincidere le origini.
Somma di due vettori v1 e v2 con il metodo grafico.
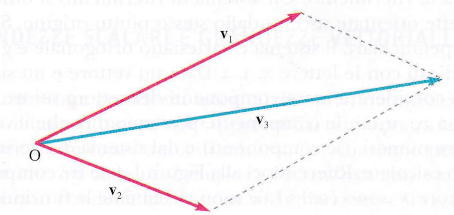
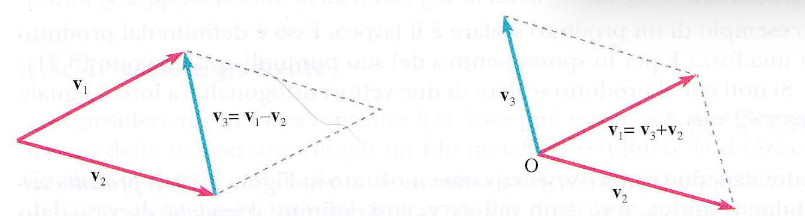
La somma dei due vettori v₁ e v₂ è il vettore v₃ = v₁ + v₂, costruito come la diagonale principale del parallelogramma che ha per lati v₁ e v₂ (vedi immagine). Per sommare più vettori, si procede sommando due vettori alla volta, applicando lo stesso metodo.
La somma vettoriale può essere eseguita anche algebricamente, utilizzando le componenti dei vettori rispetto a un determinato sistema di riferimento.
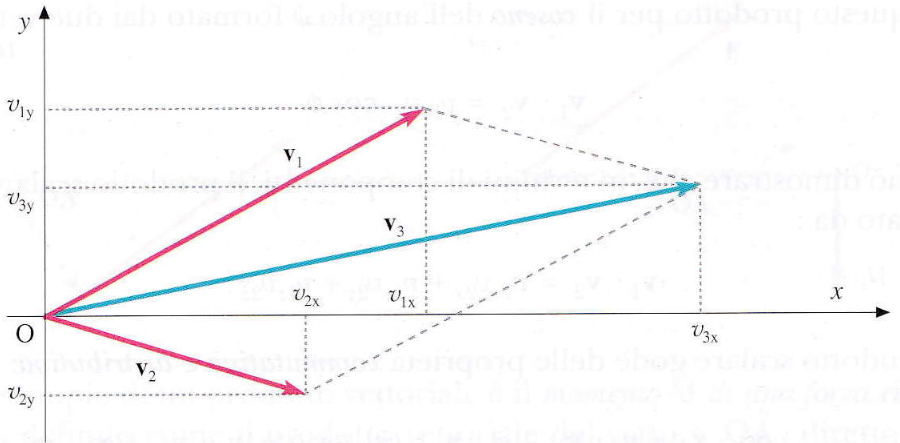
Somma di due vettori v1 e v2 con il metodo analitico (somma delle componenti omologhe):
v3x= v1x + v2x
v3y= v1y + v2y
In uno spazio tridimensionale, se:
v₁ ha componenti (v1x, v1y, v1z)
v₂ ha componenti (v2x, v2y, v2z)
allora il vettore sommav3=v1+v2 avrà componenti date da:
v3x= v1x + v2x v3y= v1y + v2y v3z= v1z + v2z
La differenza tra due vettori v₁ e v₂ è definita come il vettore v3 tale che: v1−v2=v3 ovvero v2+v3=v1.
Il vettore differenza è rappresentato dalla seconda diagonale del parallelogramma avente per lati v₁ e v₂ (vedi immagine in basso).
Differenza di due vettori v1 e v2 con il metodo grafico del parallelogramma. Se il vettore v1 avesse verso opposto, la somma v3 + v2non sarebbe iI vettore v1.
Anche la differenza può essere eseguita tramite le componenti, semplicemente sottraendo le componenti corrispondenti dei due vettori, ovvero:
v3x= v1x – v2x v3y= v1y – v2y v3z= v1z – v2z
Differenza di due vettori v1 e v2 con il metodo analitico (differenza delle componenti omologhe):
v3x= v1x – v2x
v3y= v1y – v2y
In altre parole, si utilizza la stessa formula della somma, ma con un segno meno al posto del più.
La somma di due vettori di uguale modulo e verso opposto ha per risultato un vettore nullo, cioè un vettore con tutte le componenti uguali a zero.
Prodotto scalare e prodotto vettoriale
Il prodotto scalare di due vettori v1 e v2 si ottiene moltiplicando il modulo dell’uno per Ia proiezione del primo sul secondo o viceversa.
Il prodotto di due vettori può essere definito in due modi distinti, a seconda del tipo di risultato che si vuole ottenere:
se il risultato è una quantità scalare, si parla di prodotto scalare;
se il risultato è una quantità vettoriale, si parla di prodotto vettoriale.
Dati due vettori v₁ e v₂, si definisce prodotto scalare la quantità scalare ottenuta moltiplicando:
il modulo di v₁,
il modulo di v₂,
il coseno dell’angoloϕ compreso tra i due vettori.
v1⋅v2=v1 v2 cosϕ
In termini di componenti, il prodotto scalare si calcola come:
v1⋅v2= v1xv2x + v1yv2y + v1zv2z
Il prodotto scalare gode di importanti proprietà algebriche:
commutatività: v1⋅v2= v2⋅v1
distributività rispetto alla somma: v1⋅(v2+v3)=v1⋅v2+v1⋅v3
Un tipico esempio di prodotto scalare è il lavoro L. Esso è definito come: L= F ⋅ s
Dove F è la forza e s è lo spostamento del punto di applicazione della forza.
Nota importante: il prodotto scalare tra due vettori ortogonali (perpendicolari) è nullo, poiché: cos(π/2)=0⇒v1⋅v2=0.
Dati due vettori v₁ e v₂, si definisce prodotto vettoriale un nuovo vettorev3, così calcolato:
|v3|= v1 v2 senϕ
II prodotto vettoriale dei due vettori v1 e v2 genera il vettore v3.
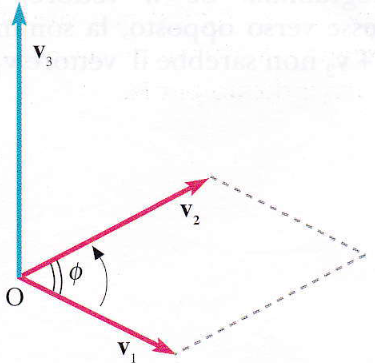
dove ϕ è l’angolo compreso tra v1 e v2. Questo valore corrisponde all’area del parallelogramma costruito sui due vettori.
La direzione è perpendicolare al piano contenente v1 e v2.
Il verso è stabilito secondo la regola della vite destrorsa: se si ruota v1verso v2 attraverso l’angolo minore (inferiore a 180°), il verso di v3 è quello in cui avanzerebbe una vite che si avvita nel senso della rotazione.
Il prodotto vettoriale si indica mediante il simbolo “×”, oppure con una “v” capovolta:
v1×v2=v3 o v1∧v2=v3
Il prodotto vettoriale può essere anche espresso in termini di componenti cartesiane:
Questo consente di calcolare il risultato numericamente, utile nelle applicazioni pratiche.
Si noti che il prodotto vettoriale:
non è commutativo, ma anticommutativo: v2 ∧ v1 =-v1∧v2
gode della proprietà distributiva: v1 ∧ (v2 + v3) = (v1 ∧ v2) + (v1 ∧ v3)
il prodotto vettoriale di due vettori paralleli è uguale al vettore nullo (sen 0° = 0).
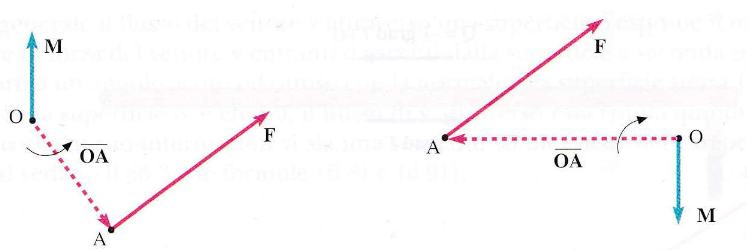
Un’applicazione classica del prodotto vettoriale è la definizione del momento M di una forza rispetto a un punto O. Dati il vettore ŌĀ che unisce il punto O al punto A di applicazione della forza e il vettore forza F, il momento è definito come:
M = ŌĀ ∧ F
Rappresentazione grafica del momento di una forza: M = ŌĀ ∧ F. Se la retta di F passa per O, il momento M è nullo. Il momento è diverso da zero se, e soltanto se, F è tale da poter produrre una rotazione intorno al punto O e il verso di M è connesso con il senso della rotazione. Per individuare il verso di M si sovrappone ŌĀ ad F (il primo vettore sul secondo, con l’angolo di rotazione minore) in modo che i loro versi coincidano. Così facendo la rotazione avviene nel senso della freccia nei due casi riportati in figura: una vite, che esegue tale rotazione, avanza nel verso indicato per M.
Il vettore gradiente
Consideriamo una funzione f(x). Essa può esprimere, ad esempio, l’andamento della temperatura lungo un filo metallico rettilineo, dove la direzione del filo fornisce l’asse x. In modo analogo, f(x) può rappresentare i valori della pressione lungo un vaso sanguigno.
Per descrivere completamente la variazione (aumento o diminuzione) della grandezza f(x) lungo la coordinata x, è necessario definire non solo l’entità della variazione stessa, ma anche una direzione e un verso. In questo modo alla variazione di f(x) si può associare un vettore. Si chiama gradiente della funzione scalare f(x) il vettore v il cui modulo è dato dalla derivata di f(x) rispetto a x, la direzione è quella dell’asse x, e il verso è quello per cui il rapporto incrementale Δf/Δx risulta positivo.
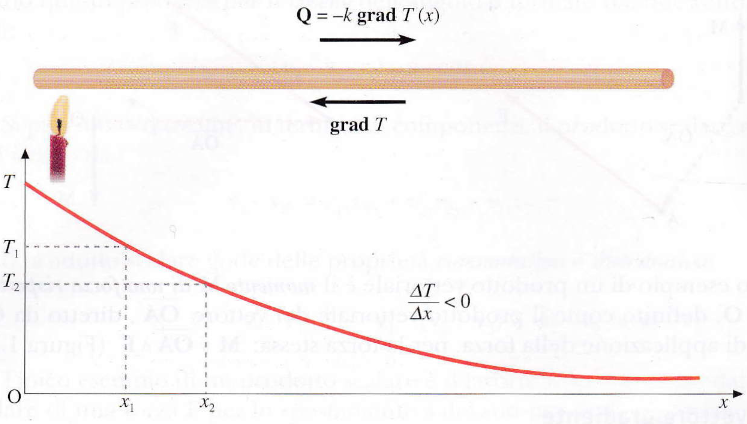
Andamento della temperatura lungo un filo rettilineo riscaldato ad un estremo. Il calore Q diffonde dalle temperature maggiori a quelle minori. Il rapporto incrementale della temperatura è negativo, per cui il verso del vettore gradiente è opposto al verso dell’asse x, da cui il segno meno introdotto per rappresentare iI vettore Q: Q=-kgrad T (x).
Ad esempio, se consideriamo il caso di un filo rettilineo riscaldato a un estremo, il calore Q diffonde lungo il filo dalle temperature maggiori a quelle minori secondo la legge: Q=k (T1−T2) / Δx, dove k è una costante e Δx è la distanza tra i punti a temperatura T1 e T2. Questa relazione può essere riscritta in forma vettoriale, attribuendo a QQQ direzione e verso del flusso di calore, utilizzando la definizione di gradiente: Q=-kgrad T (x).
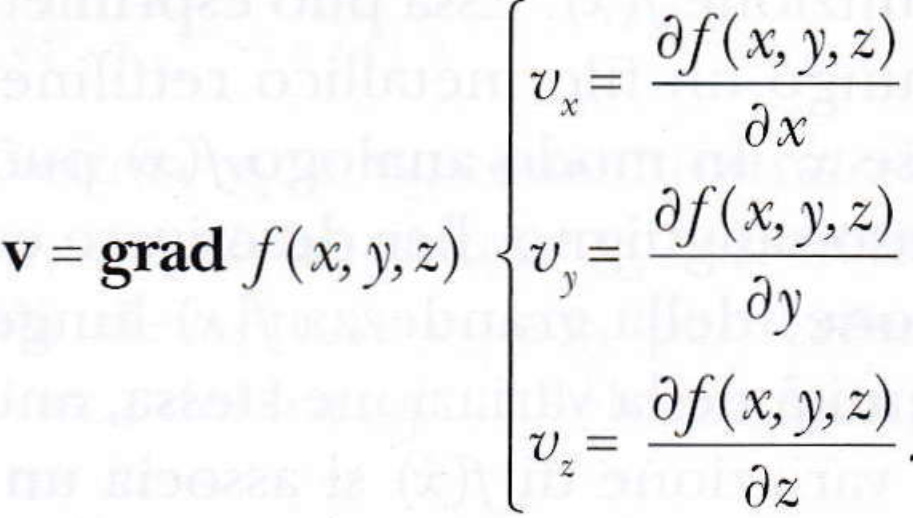
Più in generale, una grandezza fisica scalare può variare da punto a punto nello spazio (ad esempio la temperatura in un ambiente) ed essere rappresentata da una funzione f(x, y, z) dipendente da tre variabili indipendenti. In questo caso il vettore gradiente è definito tramite le derivate parziali lungo i tre assi x, y e z. Le derivate parziali sono calcolate considerando costanti le altre due coordinate.
Flusso di un vettore attraverso una superficie
In qualsiasi punto di un campo vettoriale il vettore è tangente alla linea di forza passante per il punto.
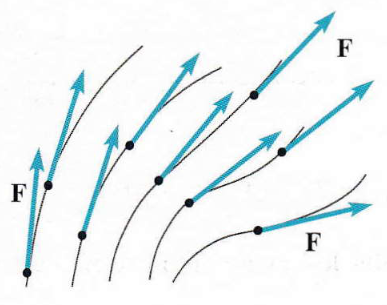
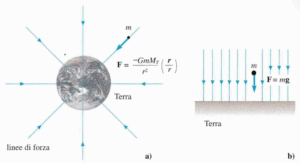
Consideriamo una regione dello spazio in cui, in ogni punto, sia definito un vettore v. Tale regione prende il nome di campo vettoriale. All’interno di questo campo si definiscono le linee di forza del vettore v come le curve tangenti, punto per punto, alla direzione di v.
Prendiamo ora una superficie S immersa in questo campo vettoriale e suddividiamola in tante piccole aree elementari si, ciascuna così piccola da poter essere approssimata come piana.
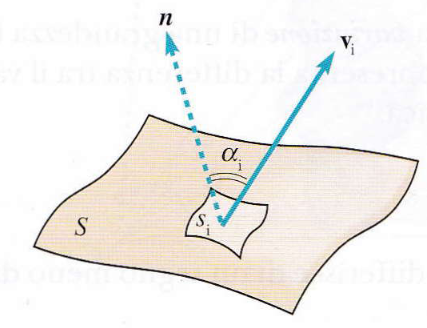
Il flusso del vettore v attraverso la superficie S viene calcolato sommando i flussi elementari attraverso Ie superfici siin cui è stata scomposta la superficie S. Le superfici sono sufficientemente piccole da poter considerare in tutti i suoi punti costanti sia il vettore v che la normale n.
Al centro di ciascuna areola consideriamo il vettore vi. Il flussoΦi del vettore vi attraverso l’areola si si ottiene come prodotto scalare tra vi e il versore ni, normale all’areola stessa, moltiplicato per l’area si:
Φi = si vi ⋅ n = si vi cos αi
dove αi è l’angolo tra il vettore vi e la normale ni.
Sommando i contributi di tutte le areole, si ottiene il flusso totale del campo vettoriale v attraverso l’intera superficie S:
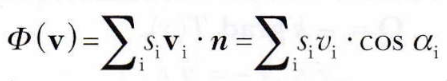
Passando al limite in cui le areole diventano infinitesime, la somma si trasforma in un integrale di superficie:
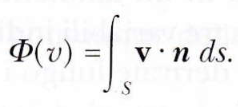
In generale, il flusso del vettore v attraverso una superficie S rappresenta il numero di linee di forza che attraversano S, in uscita o in entrata. Il segno del flusso dipende dall’angolo tra il vettore v e la normale alla superficie: se l’angolo è acuto, il flusso è positivo (linee uscenti); se è ottuso, il flusso è negativo (linee entranti), come illustrato nell’immagine in alto a destra.
Nel caso in cui la superficie S sia chiusa, il flusso attraverso essa risulta nullo, a meno che al suo interno non sia presente una sorgente (o una cavità) del campo vettoriale.
