La Meccanica Classica, nota anche come Meccanica Newtoniana, è la branca della fisica che descrive il moto dei corpi macroscopici. Essa fornisce un quadro teorico robusto e predittivo per analizzare il comportamento di oggetti che vanno dai proiettili ai pianeti. È fondamentale, tuttavia, delinearne i confini di validità: la Meccanica Classica non si applica allo studio dei fenomeni su scala atomica, i quali sono oggetto della Meccanica Quantistica, né a quelli che coinvolgono corpi in movimento a velocità prossime a quella della luce, dominio della Teoria della Relatività.
Il punto di partenza per l’analisi dello stato di moto dei corpi è il concetto di forza.
Per costruire un’analisi rigorosa del moto, è indispensabile superare la nozione intuitiva di forza per approdare a una definizione fisica chiara e operativa. Questo passaggio permette di quantificare le interazioni tra i corpi e di prevederne le conseguenze dinamiche in modo sistematico.
L’idea primordiale di forza deriva dall’esperienza diretta dello “sforzo muscolare“. L’osservazione quotidiana mostra che applicando uno sforzo a un oggetto, si ottengono due possibili effetti: se il corpo è libero di muoversi, esso si mette in movimento; se è vincolato, subisce una deformazione. Partendo da questa constatazione, si astrae il concetto per arrivare a una definizione più generale.
In fisica, una forza è definita come l’agente fisico in grado di causare un’accelerazione, ovvero un cambiamento nello stato di moto di un corpo. Come effetto osservabile, una forza applicata a un corpo vincolato può anche causarne la deformazione.
Esistono diverse tipologie di forze in natura, tra cui:
forza peso: la forza di attrazione gravitazionale esercitata dalla Terra su un corpo;
forza muscolare: la forza generata dalla contrazione dei fasci muscolari;
forza elastica: la forza di reazione di un corpo elastico che si oppone a una deformazione;
forze elettriche e magnetiche: forze che agiscono tra cariche elettriche e magneti.
Le forze sono grandezze vettoriali. La loro azione non è completamente descritta dalla sola intensità (modulo), ma richiede anche la specificazione di una direzione e di un verso. Di conseguenza, la loro composizione e scomposizione segue le regole del calcolo vettoriale.
Per la misurazione delle forze si possono adottare due approcci distinti:
metodo statico: si basa sulla misurazione della deformazione prodotta su un corpo campione, come l’allungamento di una molla calibrata all’interno di un dinamometro;
metodo dinamico: si basa sull’osservazione degli effetti della forza sullo stato di moto di un corpo, ovvero misurando l’accelerazione che essa produce. Questo metodo trova la sua piena formalizzazione nel secondo principio della dinamica.
I principi della dinamica forniranno il quadro sistematico per comprendere appieno la relazione tra le forze e il movimento, unificando questi concetti in un corpo di leggi coerente.
I principi fondamentali della dinamica
I tre principi della dinamica, formulati da Isaac Newton, sono i pilastri su cui si fonda l’intera Meccanica Classica. Essi stabiliscono in modo inequivocabile le leggi che governano il moto dei corpi in risposta alle forze applicate, collegando i concetti di forza, massa e accelerazione.
Primo principio: la legge d’inerzia
Il primo principio della dinamica, o principio d’inerzia, afferma che:
Ogni corpo persevera nel proprio stato di quiete o di moto rettilineo uniforme, finché forze esterne ad esso non intervengano a modificarne lo stato di moto
L’implicazione fondamentale è che un corpo non modifica spontaneamente il proprio stato di moto. In assenza di una forza netta esterna, un oggetto fermo rimane fermo e un oggetto in movimento continua a muoversi a velocità costante lungo una linea retta.
L’enunciazione di questo principio, insieme al secondo, solleva immediatamente la questione del sistema di riferimento per due ragioni fondamentali. La prima è di natura cinematica: grandezze come la quiete e la velocità hanno significato solo se definite rispetto a un osservatore. La seconda, più profonda e dettata dalla fisica stessa, è che la validità delle leggi della dinamica dipende intrinsecamente dalla scelta del sistema di riferimento.
Vengono definiti sistemi di riferimento inerziali quei sistemi in cui il principio d’inerzia è valido. Esempi di tali sistemi sono quelli solidali con le “stelle fisse” o qualsiasi altro sistema che si muova di moto traslatorio uniforme rispetto a esse. Al contrario, un sistema in rotazione, come una piattaforma girevole, non è inerziale. Per la maggior parte dei fenomeni che si svolgono in regioni limitate della superficie terrestre, il sistema di riferimento solidale con la Terra può essere considerato, con ottima approssimazione, un sistema inerziale.
Secondo principio: la relazione fondamentale F = ma
Il secondo principio della dinamica stabilisce una relazione quantitativa diretta tra la forza applicata a un corpo e l’accelerazione che ne risulta. Esso enuncia che l’accelerazione subita da un corpo è direttamente proporzionale alla forza totale agente su di esso.
Questa relazione è espressa dalla formula fondamentale della dinamica:
F = ma
In questa equazione:
F è la forza netta (vettoriale) applicata al corpo;
a è l’accelerazione (vettoriale) prodotta;
m è la costante di proporzionalità, detta massa inerziale.
La massa inerziale (m) è una proprietà intrinseca e scalare del corpo. Essa misura la sua inerzia, ovvero la sua resistenza a subire un’accelerazione quando soggetta a una forza. A parità di forza applicata, un corpo con massa maggiore subirà un’accelerazione minore. In senso più fondamentale, può essere considerata una misura della quantità di materia del corpo.
Questa legge fornisce anche una definizione dinamica della forza: il valore di una forza può essere determinato misurando la massa del corpo su cui agisce e l’accelerazione che essa produce.
Nel Sistema Internazionale (S.I.), l’unità di misura della forza è il newton (N), definito come la forza necessaria per imprimere a una massa di 1 kg un’accelerazione di 1 m/s².
Terzo principio: azione e reazione
Il terzo principio della dinamica, o principio di azione e reazione, descrive la natura delle interazioni tra corpi. Esso afferma che:
Se un corpo A esercita una forza F su un corpo B, allora il corpo B esercita simultaneamente sul corpo A una forza -F.
La forza esercitata da B su A (la “reazione”) possiede le seguenti caratteristiche rispetto alla forza esercitata da A su B (l'”azione”):
ha lo stesso modulo (intensità);
agisce lungo la stessa direzione e la stessa retta di applicazione;
ha verso opposto.
Questo principio è fondamentale per lo studio dei sistemi composti da più corpi interagenti e, come vedremo, porta direttamente a una delle più importanti leggi di conservazione della fisica.
Quantità di moto
Dai principi fondamentali della dinamica, e in particolare dalla combinazione del secondo e del terzo, emergono concetti derivati e teoremi di enorme importanza pratica e teorica. Tra questi, il più significativo è la quantità di moto e la sua associata legge di conservazione.
Si definisce quantità di moto (q) di un corpo la grandezza vettoriale data dal prodotto della sua massa m per la sua velocità v:
q = mv
Il secondo principio della dinamica può essere espresso nella sua forma più generale e fondamentale in termini di quantità di moto:
F = dq/dt
Questa formulazione afferma che la forza netta agente su un corpo è uguale alla variazione della sua quantità di moto nel tempo. La sua importanza risiede nel fatto che rimane valida anche in sistemi a massa variabile (come un razzo che espelle carburante). Nel caso specifico in cui la massa m del corpo sia costante, questa legge si semplifica nella forma più nota. Infatti:
F = d(mv)/dt = m(dv/dt) = ma
Il teorema di conservazione della quantità di Moto
Un sistema isolato è definito come un sistema di corpi soggetto unicamente a forze interne, ovvero le forze che i corpi del sistema si scambiano reciprocamente. Per tali sistemi, vale il seguente teorema.
Interazione tra corpi su piano orizzontale: azione, reazione e quantità di moto
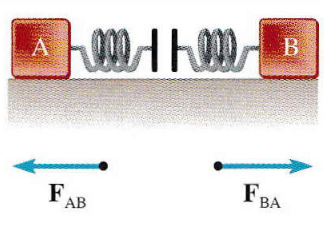
Il teorema di conservazione della quantità di moto afferma che in un sistema isolato, la quantità di moto totale del sistema rimane costante nel tempo.
Questa legge è una conseguenza diretta del terzo principio di Newton. Considerando un sistema isolato composto da due corpi A e B, la forza che A esercita su B (FAB) è uguale e contraria a quella che B esercita su A (FBA). Poiché le due forze agiscono per lo stesso intervallo di tempo, anche gli impulsi da esse prodotti sono uguali e opposti. Dal momento che l’impulso corrisponde alla variazione della quantità di moto, ne consegue che ΔqA = -ΔqB. La variazione totale della quantità di moto del sistema è quindi nulla:
Un esempio classico che illustra questo principio è il cannone che rincula. Il sistema è costituito dal cannone e dal proiettile. Prima dello sparo, entrambi sono fermi e la quantità di moto totale è zero. Quando il proiettile viene espulso, acquista una grande quantità di moto in una direzione. Per conservare la quantità di moto totale del sistema a zero, il cannone deve acquisire una quantità di moto uguale in modulo ma di verso opposto, manifestando il fenomeno del rinculo.
La legge di conservazione della quantità di moto si rivela così uno strumento analitico essenziale per studiare urti, esplosioni e altre interazioni all’interno di sistemi isolati.
