Il processo di diffusione è un processo di flusso di gas e soluti da un compartimento a maggior concentrazione ad uno a minore concentrazione fino a raggiungere l’equilibrio dinamico.
Le particelle solide in diffusione si muovono casualmente urtandosi tra di loro secondo un fenomeno chiamato agitazione termica che dipende soprattutto dalla temperatura. L’agitazione termica è chiamata anche moto Browniano ed è il principale responsabile della diffusione di particelle (molecole o strutture più complesse) in un ambiente libero o attraverso una membrana.
Le leggi che stabiliscono delle relazioni tra flussi e concentrazioni sono le leggi di Fick. La prima legge afferma che il flusso di soluto Js è direttamente proporzionale alla variazione di concentrazione ΔC tra i due compartimenti e inversamente proporzionale alla distanza Δx tra i due:
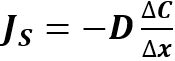
Il segno negativo indica che il fluire del soluto procede sempre da concentrazioni maggiori a quelle minori mentre D rappresenta il coefficiente di diffusione che dipende dalla temperatura e dalle caratteristiche fisico-chimiche del solvente e del soluto. L’unità di misura del coefficiente di diffusione è il m2/s nel sistema internazionale.
Tuttavia la diffusione di soluto procede fino a che il soluto si è distribuito in modo omogeneo nel solvente. Quindi il flusso di soluto continua a variare nel tempo fino a Js=0, quando la concentrazione ha lo stesso valore in ogni punto della soluzione e si raggiunge un equilibrio dinamico.
Ciò è regolato dalla seconda legge di Fick:
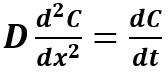
Questa legge viene applicata solo quando la concentrazione varia nel tempo ed è una equazione differenziale omogenea del 2° ordine che lega tra loro le variazioni di C in funzione di x e del tempo.
Nel caso della diffusione libera di miscele gassose, ipotizzando che i gas si comportino come gas perfetti, le leggi di Fick possono essere riformulate prendendo in considerazione l’equazione di stato dei gas perfetti, per cui la concentrazione diventa:
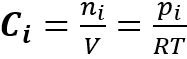
Inoltre, considerando che la T nei sistemi biologici è costante, le due leggi di Fick diventano:
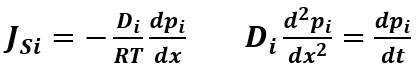
Quando invece si considera la diffusione attraverso la membrana nella prima legge di Fick bisogna considerare il coefficiente di partizione α che rappresenta il rapporto fra l’area aperta al passaggio di sostanze e l’area totale della membrana. Esso è un indice della permeabilità di una membrana. Se α=0 la membrana è impermeabile al soluto, se α=1 è come se non esistesse. Quindi la prima legge di Fick diventa:

Dove JsM è il flusso di soluto attraverso la membrana, DM è il coefficiente di diffusione attraverso la membrana e Δx lo spessore della membrana stessa.
Importante per capire il flusso di soluto in funzione della variazione di concentrazione è la definizione di permeabilità:
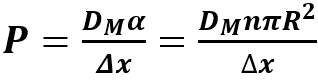
Dove n = NA/A è la densità superficiale dei fori della membrana mentre R è il raggio del poro.
Per cui la prima legge di Fick diventa: JsM= -P ΔC
Now loading…
Per quanto riguarda la seconda legge di Fick, essa rimane la stessa per la diffusione mediante membrane e non viene mai applicata alle membrane biologiche in quanto esse separano soluzioni omeostatiche la cui composizione rimane costante nel tempo. Infatti anche se si hanno flussi continui, uno dei due compartimenti viene continuamente approvvigionato di soluto mentre nell’altro compartimento viene consumato.
Per il fenomeno di diffusione molto importante è il coefficiente di diffusione D, le cui caratteristiche sono determinate dalla formula di Einstein-Stokes:
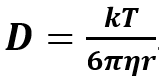
Nel caso del coefficiente di diffusione attraverso una membrana DM, esso può essere messo in relazione con quello libero osservando che la molecola di raggio r, per attraversare la membrana deve introdursi in uno dei suoi pori di raggio R senza urtare il bordo, quindi l’area di ingresso efficace è π (R-r)2. E quindi l’area efficace diventa π R2ε1. Dove ε1= (1-r/R)2 rappresenta la riduzione di D causata dalla forma del poro della membrana ed è compreso tra 0 e 1.
Inoltre, gli urti che la molecola subisce con le pareti cilindriche fanno ridurre il coefficiente D di un fattore ε2 in funzione del rapporto r/R. Entrambi i fattori sono inglobati nel coefficiente di hindrance della membrana: ε=ε1ε2. Quindi DM=εD
Considerando il coefficiente di hindrance, la permeabilità di membrana diventa:
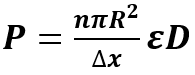
Fonte: Fisica biomedica.