Quando un fluido reale si muove in un condotto, a differenza dei fluidi ideali, si ha a che fare con delle forze di attrito che ostacolano il moto del fluido dovute alle forze di coesione tra le molecole che, in un condotto, aumentano dall’interno del fluido verso la parete del condotto. Quindi la velocità di scorrimento del liquido aumenta in modo concentrico verso il centro del condotto cilindrico.

Considerando un cilindro di fluido di raggio r, con superficie laterale S, che scorre a velocità v + Δv e su di esso scorre un secondo strato di cilindro con velocità v e raggio r + Δr. Sperimentalmente si osserva che la forza di attrito F tra due strati contigui è proporzionale alla superficie S ed alla differenza di velocità Δv ed è inversamente proporzionale a Δr tra i due cilindri concentrici:
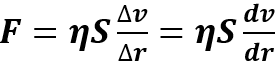
dove dv/dr è chiamato gradiente di velocità mentre η è il coefficiente di viscosità che varia con il tipo di liquido, con la temperatura e la pressione. Infatti diminuisce all’aumentare della T e cresce all’aumentare della pressione:
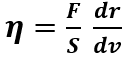
La sua unità di misura è il Pa s.
A causa della loro viscosità, i liquidi reali scorrono perdendo parte della loro energia meccanica per trasformarla in energia interna con aumento della temperatura.
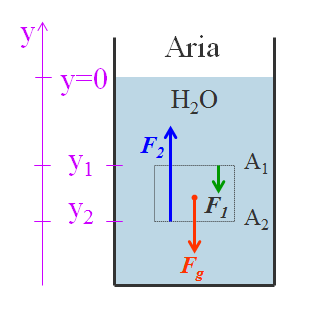
Se consideriamo l’energia meccanica persa per unità di volume ε del liquido tra due sezioni del condotto, nel teorema di Bernoulli si ha:
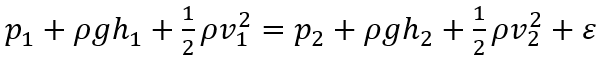
Se h1=h2 e v1=v2 allora p1=p2+ε e quindi ε =p1-p2.
Da questa assunzione si capische che affinché un fluido con attrito viscoso possa scorrere con moto laminare o stazionario a portata costante in un condotto orizzontale, deve essere applicata una differenza di pressione Δp ai suoi estremi per vincere le forze di attrito. Il valore di questa differenza di pressione è ricavabile dalla legge di Poiseuille valida per tubi cilindrici di raggio r, lunghezza l e portata Q in cui il moto del fluido è laminare:

Da questa equazione si può notare come Δp tra due sezioni distanti l di un tubo orizzontale è inversamente proporzionale a r4. Quindi più è piccola la sezione di un tubo, maggiore sarà la caduta di pressione Δp. Perciò, per mantenere costante la portata Q di un fluido reale che scorre in un tubo orizzontale si deve applicare con una pompa una Δp di circa 1/r4. Questo significa che se r di un tubo si dimezza, la Δp deve aumentare di 16 volte per mantenere la stessa portata Q.
Dimostrazione della legge di Poiseuille
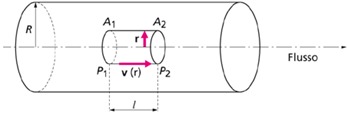
Per dimostrare la legge di Poiseuille si consideri all’interno di un tubo di raggio R, un cilindro di raggio r e lunghezza l che si muove con velocità v(r).
Sulle basi del cilindro agiscono delle forze di pressione Fp la cui risultante è: Fp= πr2 (p1-p2). Inoltre, il moto del cilindro è rallentato dalle forze di attrito viscoso Fη che agiscono sulla superficie laterale di area 2πrl per cui:
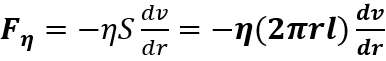
dove il segno negativo indica che la forza è opposta al moto del cilindro.
Poiché il cilindro si muove a velocità costante e ciò avviene solo quando la somma delle forze è nulla Fp + Fη = 0 allora:
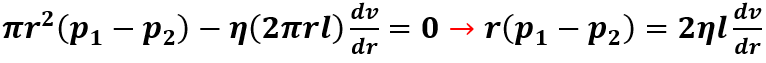
tuttavia dv/dr < 0 quindi:
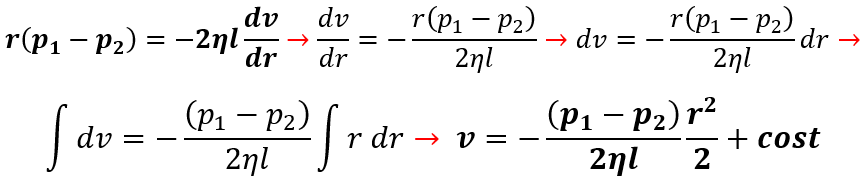
Adesso si determina la costante di integrazione considerando r=R, dove v=0:
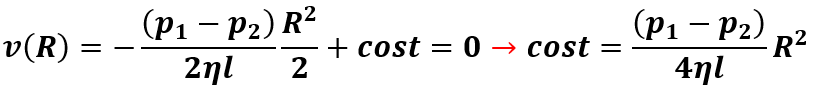
Si avrà allora che:
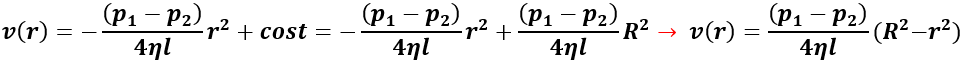
Considerando adesso l’asse del tubo e quindi r=0, dove v=vmax

La velocità media con cui scorre il fluido nel tubo sarà quindi:
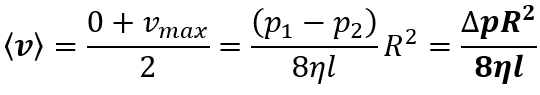
Dall’equazione di continuità (legge di Leonardo) Q= A<v>allora:
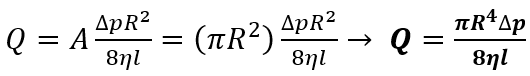
L’equazione ottenuta non è altro che la legge di Poiseuille.
Fonte: Fisica biomedica.