Analisi della dinamica traslatoria: dalle forze alla Legge Oraria

Questo articolo si propone di illustrare il procedimento formale attraverso cui è possibile determinare l’espressione esplicita della legge oraria di un corpo, partendo dalla conoscenza del campo di forze a cui esso è soggetto. Questo nesso di causalità tra la forza, intesa come causa della variazione del moto, e l’accelerazione, che ne descrive l’effetto, rappresenta uno dei pilastri fondamentali delle leggi della Dinamica. La relazione tra questi due elementi è mediata da una proprietà intrinseca del corpo, la sua massa inerziale m, che ne quantifica la resistenza a variare il proprio stato di moto.

Per dimostrare la validità e l’universalità di questo approccio, verranno analizzati alcuni casi paradigmatici della fisica: il moto in assenza di forze (inerziale), sotto l’azione di una forza uniforme (come nel campo gravitazionale locale), in un campo di forze centrale e, infine, quello generato da una forza di tipo elastico. Ciascuno di questi scenari, pur partendo da presupposti fisici differenti, verrà risolto applicando un’unica metodologia rigorosa.

Il nucleo metodologico dell’articolo si basa sull’integrazione dell’equazione del moto, un’equazione differenziale che traduce in termini matematici il Secondo Principio della Dinamica, permettendo di predire l’evoluzione temporale di qualunque sistema meccanico una volta note le forze in gioco e lo stato iniziale del sistema.

Dall’equazione di moto alle condizioni iniziali

Il passaggio dalla descrizione delle forze alla determinazione della traiettoria di un corpo segue un percorso analitico preciso. Il Secondo Principio della Dinamica, F = ma, non è una semplice formula algebrica, ma un’equazione differenziale di secondo ordine. Essa racchiude la relazione profonda e continua tra la causa, la forza F, e l’effetto cinematico, ovvero la variazione istantanea del moto descritta dall’accelerazione a. Risolvere questa equazione significa, di fatto, decodificare l’intera evoluzione temporale del sistema.

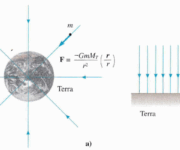
Si consideri un campo di forze stazionario, ovvero indipendente dal tempo, in cui il vettore forza F è una funzione nota della posizione (x, y, z):

$F = F(x, y, z)$

Il Secondo Principio della Dinamica stabilisce un legame istantaneo tra questa forza e l’accelerazione del corpo di massa m. Esplicitando l’accelerazione come la derivata seconda della posizione rispetto al tempo e proiettando l’equazione vettoriale lungo gli assi di un sistema cartesiano ortogonale, si ottiene un sistema di tre equazioni differenziali scalari:

\mathbf{F} = m\mathbf{a} \left\{ \begin{aligned} F_x &= m a_x = m \frac{d^2x}{dt^2} \\ F_y &= m a_y = m \frac{d^2y}{dt^2} \\ F_z &= m a_z = m \frac{d^2z}{dt^2} \end{aligned} \right.

La soluzione di questo sistema non è un valore numerico, ma un insieme di tre funzioni del tempo, x(t), y(t) e z(t), che nel loro insieme costituiscono la legge oraria del moto. Queste funzioni descrivono in modo completo la posizione del corpo in ogni istante.

La soluzione del sistema di equazioni non è, in generale, univoca. L’operazione di derivata seconda, infatti, elimina qualsiasi informazione relativa a termini costanti o lineari nella funzione di partenza. Di conseguenza, il processo inverso di integrazione non può ricostruire questi termini senza informazioni aggiuntive. Per ottenere una soluzione determinata, è necessario imporre delle condizioni specifiche al moto.

Queste informazioni sono note come condizioni iniziali e consistono nella conoscenza esatta della posizione e della velocità del corpo in un preciso istante di tempo, convenzionalmente t=0. Formalmente, esse sono definite dai vettori:

posizione iniziale: s₀, con componenti (x₀, y₀, z₀);
velocità iniziale: v₀, con componenti (v₀ₓ, v₀ᵧ, v₀_z).

Questi sei valori scalari corrispondono alle costanti arbitrarie che emergono dal processo di doppia integrazione delle tre equazioni del sistema. Imponendo queste condizioni, si seleziona, tra tutte le infinite traiettorie possibili, l’unica che descrive il moto effettivo del corpo in esame, rendendo la soluzione univoca.

Questo apparato formale, che lega forze, equazione differenziale e condizioni iniziali, verrà ora applicato a scenari fisici concreti e fondamentali.

Applicazione del metodo a campi di forze noti

Dopo aver definito il metodo generale, si procede ora ad applicarlo a quattro tipologie di campi di forze fondamentali in fisica. Ciascuno di questi casi, pur essendo un’idealizzazione, descrive con eccellente approssimazione un’ampia gamma di fenomeni reali e dimostra come la natura della forza determini in modo univoco la classe di moto che ne consegue.

Moto inerziale in assenza di forze (F = 0)

Il caso più semplice è quello di un corpo non soggetto ad alcuna forza netta, ovvero F = 0. In questa condizione, il sistema di equazioni si semplifica notevolmente, poiché le componenti F_x, F_y e F_z sono tutte nulle. Integrando due volte rispetto al tempo ciascuna equazione, si ottiene la soluzione generale:

x = x_0 + v_{0x}t

y = y_0 + v_{0y}t

z = z_0 + v_{0z}t

L’interpretazione fisica di queste equazioni è immediata: esse rappresentano la legge oraria del moto rettilineo uniforme. Le costanti di integrazione (x₀, y₀, z₀) e (v₀ₓ, v₀ᵧ, v₀₂) corrispondono esattamente alle componenti della posizione e della velocità del corpo all’istante iniziale t=0. Scegliendo un sistema di riferimento con l’asse x allineato alla velocità iniziale, la legge oraria assume la forma semplificata:

\mathbf{x(t) = x_0 + v_0t}

Moto in un campo di forze uniforme (F = costante)

Si consideri un campo di forze costante in modulo, direzione e verso in ogni punto dello spazio: F = F₀. Un esempio fisico di grande importanza è il campo gravitazionale terrestre in prossimità del suolo. Si orienti il sistema di riferimento in modo che la forza agisca unicamente lungo l’asse y. Le equazioni di moto si semplificano in:

\begin{array}{l} \textbf{ Asse x: } 0 = m \frac{d^2x}{dt^2} \quad (\text{accelerazione nulla}) \\[1em] \textbf{ Asse y: } F_{oy} = F_o = m \frac{d^2y}{dt^2} \quad (\text{forza costante}) \end{array}

La soluzione per la componente x è identica a quella del moto inerziale, poiché lungo tale asse non agiscono forze:

\boldsymbol{x(t) = x_0 + v_{0x}t}

Per la componente y, si procede con una doppia integrazione. La prima integrazione dell’equazione d²y/dt² = F₀/m fornisce l’andamento della velocità vᵧ(t):

{v_y(t) = \frac{F_0}{m}t + v_{0y}} \\[1em]

dove v₀ᵧ è la costante di integrazione, ovvero la componente y della velocità iniziale. Una seconda integrazione fornisce la posizione y(t):

\boldsymbol{y(t) = \frac{1}{2} \frac{F_0}{m} t^2 + v_{0y}t + y_0}

Le funzioni evidenziate in grassetto descrivono la legge oraria del moto uniformemente accelerato. La traiettoria del corpo è rettilinea se la velocità orizzontale iniziale (v_ox) è zero, una parabola in tutti gli altri casi.

Il moto parabolico

Un’applicazione diretta del moto in un campo di forze uniforme è il moto di un proiettile nel campo gravitazionale terrestre (trascurando la resistenza dell’aria). La forza agente è il peso p = mg, costante e diretta verticalmente verso il basso.

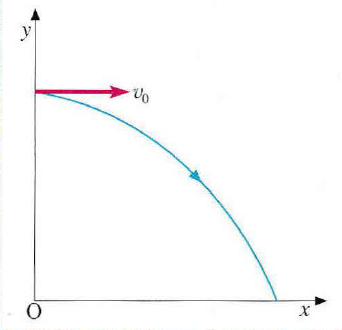
Come nell’immagine accanto, si consideri un corpo lanciato da un’altezza h con una velocità iniziale v₀ puramente orizzontale. Ponendo l’origine degli assi al suolo, le condizioni iniziali sono (x₀=0, y₀=h) e (v₀ₓ=v₀, v₀ᵧ=0). L’accelerazione ha componenti aₓ=0 e aᵧ=-g. Sostituendo questi valori nelle leggi orarie si ottiene:

\begin{cases} x(t) = v_0 t \\ y(t) = h – \frac{1}{2}gt^2 \end{cases}

Ricavando il tempo t dalla prima equazione (t = x/v₀) e sostituendolo nella seconda, si ottiene l’equazione della traiettoria, che lega direttamente la coordinata y alla x:

\boldsymbol{y(x) = h – \frac{gx^2}{2v_0^2}}

Questa è l’equazione di una parabola con la concavità rivolta verso il basso, dimostrando che la traiettoria del corpo è un arco di parabola.

Moto in un campo di forze centrale

Un campo di forze si definisce centrale quando la forza è, in ogni punto dello spazio, diretta verso un punto fisso O, detto centro. L’integrazione delle equazioni di moto in un campo centrale generico risulta complessa. Basti ricordare che per un campo gravitazionale, che varia con l’inverso del quadrato della distanza, si ottengono come traiettorie generali le sezioni coniche, in particolare le traiettorie ellittiche tipiche dei pianeti del sistema solare.

Ci si limita qui a considerare un caso particolare di grande rilevanza: quello in cui si realizza un moto circolare. Ciò avviene a condizioni molto specifiche: la velocità iniziale v del corpo deve essere esattamente perpendicolare alla forza F e il suo modulo deve soddisfare una precisa relazione. In questa configurazione, le componenti dell’accelerazione sono:

ma_T = m \frac{dv}{dt} = F_T = 0

ma_N = m \frac{v^2}{R} = F_N = F

Dalla prima equazione si deduce che il modulo della velocità v rimane costante. La seconda equazione stabilisce la condizione per cui il moto si mantenga su una circonferenza di raggio R. Se la forza F, che può dipendere dalla distanza R, soddisfa questa relazione, si realizza un moto circolare uniforme. La condizione fondamentale è:

m \frac{v^2}{R} = F(R)

Questa equazione determina il raggio R della traiettoria circolare stabile, date la massa, la velocità del corpo e la natura della forza centrale F(R).

Moto in un campo di forze elastiche (moto armonico)

Si considera una forza di tipo elastico, la cui intensità è proporzionale allo spostamento x da una posizione di equilibrio e diretta in verso opposto allo spostamento stesso. Tale forza è descritta dalla Legge di Hooke:

$F = -kx$

dove k è la costante elastica. Sostituendo questa espressione nell’equazione di moto, si ottiene l’equazione differenziale del moto:

m \frac{d^2x}{dt^2} = -kx \\[1em]

Questa equazione non è risolvibile mediante semplice integrazione, ma per via analitica. Si ricerca una funzione x(t) tale che la sua derivata seconda sia proporzionale alla funzione stessa cambiata di segno. Le funzioni che possiedono questa specifica proprietà sono le funzioni trigonometriche seno e coseno. Si assume quindi come soluzione generale una funzione sinusoidale:

x(t) = A sen(ωt + φ)

Per verificare che sia una soluzione valida e per determinare il parametro ω, si deriva due volte x(t) e si sostituisce nell’equazione di moto:

-Amω²sen(ωt + φ) = -kAsen(ωt + φ)

Questa uguaglianza è soddisfatta per ogni istante t se i coefficienti sono uguali, ovvero se mω² = k. Da ciò si ricava la pulsazione ω, che dipende unicamente dalle proprietà fisiche del sistema:

\omega^2 = \frac{k}{m}, \text{ cioè } \omega = \sqrt{\frac{k}{m}}.

I parametri della soluzione hanno dunque un significato fisico preciso:

A (ampiezza) e φ (fase iniziale) sono le due costanti di integrazione, determinate dalle condizioni iniziali;
ω (pulsazione) è una grandezza intrinseca del sistema.

Il moto risultante è il moto armonico semplice. Si noti che la legge oraria può essere rappresentata in modo equivalente da una funzione coseno, con una fase iniziale φ variata di π/2.

Conclusioni

Questa analisi ha dimostrato come il Secondo Principio della Dinamica, interpretato come un’equazione differenziale, fornisca un metodo universale per predire l’evoluzione temporale del moto di un corpo. Il procedimento richiede la conoscenza di due elementi fondamentali: la natura delle forze agenti, che determina la struttura dell’equazione, e le condizioni iniziali di posizione e velocità, che ne specificano la soluzione univoca.

L’analisi dei casi fondamentali ha evidenziato una corrispondenza diretta e qualitativa tra il tipo di forza e la cinematica risultante:

una forza nulla (F=0) genera un moto rettilineo uniforme;
una forza costante (F=cost) genera un moto uniformemente accelerato, con traiettoria tipicamente parabolica;
una forza centrale, in condizioni specifiche, genera un moto circolare uniforme, mentre nel caso generale (gravitazionale) produce orbite ellittiche;
una forza elastica (F=-kx) genera un moto armonico semplice, di natura oscillante.

Questo approccio deterministico costituisce il fondamento della meccanica predittiva, un paradigma che, ben oltre i casi esaminati, permette di analizzare e prevedere il comportamento di una vasta gamma di sistemi fisici, dal moto dei pianeti alle oscillazioni delle strutture ingegneristiche.