La meccanica rappresenta la branca della fisica dedicata allo studio del moto dei corpi e delle forze che ne determinano il comportamento. Tradizionalmente, essa viene suddivisa in tre discipline complementari:
- la cinematica, che descrive il movimento a prescindere dalle cause che lo generano;
- la dinamica, che mette in relazione le forze applicate con le conseguenti variazioni dello stato di moto;
- la statica, che analizza le condizioni di equilibrio.
In questo articolo ci concentriamo sui principi fondamentali della cinematica, il cui studio costituisce il prerequisito indispensabile per qualsiasi successiva analisi dinamica e, di conseguenza, per la progettazione e la verifica di sistemi meccanici.
Si precisa che l’analisi assume come modello di riferimento il punto materiale. Tuttavia, le leggi descritte possono essere estese con piena validità anche al moto del baricentro di un corpo rigido esteso, considerato non deformabile sotto l’azione di forze esterne.
Per intraprendere tale analisi, è indispensabile definire con rigore le grandezze fisiche e matematiche che permettono di quantificare il moto in modo univoco e oggettivo.
Caricamento…
Le grandezze fondamentali del moto
La descrizione rigorosa del moto di un corpo richiede, in primo luogo, la definizione di un sistema di riferimento fisso e, successivamente, l’introduzione di un insieme di grandezze matematiche precise. Queste grandezze (la traiettoria, la legge oraria, la velocità e l’accelerazione) costituiscono il linguaggio formale della cinematica, permettendo di tradurre un fenomeno fisico in un modello analitico.
Caricamento….
Si definisce traiettoria la linea geometrica descritta dal punto materiale durante il suo movimento nello spazio.
La legge oraria è la relazione funzionale che lega la posizione del punto sulla traiettoria all’istante di tempo. Indicando con s la distanza percorsa lungo la traiettoria, la legge oraria si esprime come:
s = s(t)
In un sistema di riferimento cartesiano tridimensionale, la legge oraria viene espressa attraverso le sue componenti, ovvero le tre funzioni parametriche che descrivono le coordinate del punto in funzione del tempo:
x = x(t);y = y(t);z = z(t).
La conoscenza di queste funzioni permette di determinare la posizione del corpo in qualsiasi istante e, implicitamente, di ricostruire la sua traiettoria.
La velocità è la grandezza che descrive la rapidità con cui varia la posizione di un corpo nel tempo. È necessario distinguere tra le sue definizioni scalari e vettoriali:
- velocità scalare media: è definita come il rapporto tra lo spazio percorso
Δse l’intervallo di tempoΔtimpiegato a percorrerlo:vmedia = Δs / Δt - velocità scalare istantanea: rappresenta il valore limite a cui tende la velocità media quando l’intervallo di tempo
Δttende a zero. Matematicamente, corrisponde alla derivata prima dello spazio rispetto al tempo.v = ds / dt
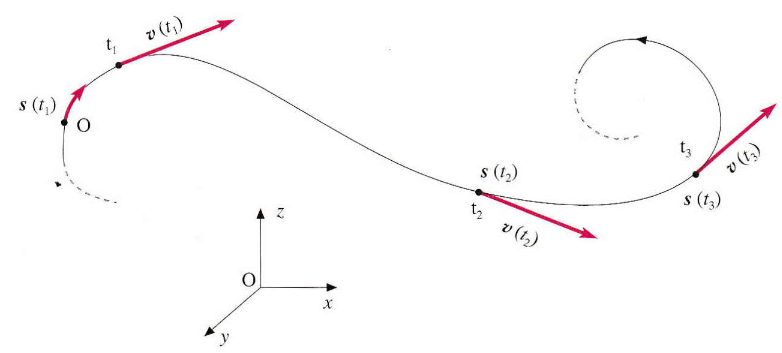
Dal punto di vista geometrico, la velocità istantanea rappresenta la pendenza della retta tangente al grafico spazio-tempo nell’istante considerato; - velocità vettoriale: per una descrizione completa, la velocità deve essere trattata come un vettore. Il vettore velocità istantanea
vè definito come la derivata del vettore spostamentosrispetto al tempo.v = ds / dt
Questo vettore possiede un modulo pari alla velocità scalare istantanea ed è sempre diretto tangenzialmente alla traiettoria nel punto considerato, con verso concorde a quello del moto.
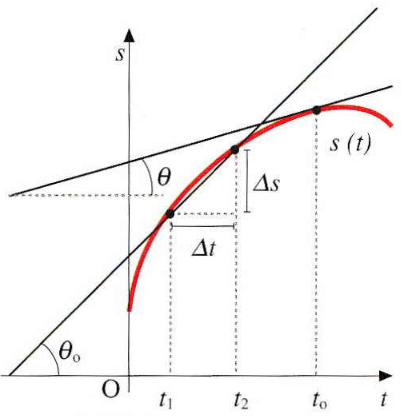
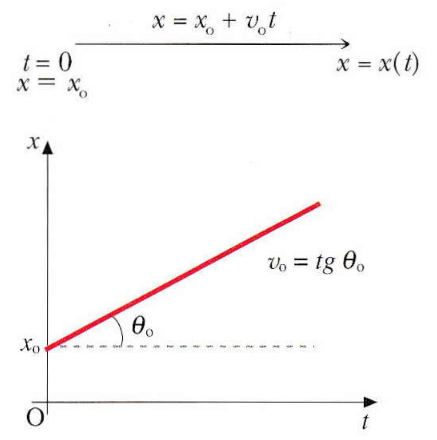
Nel grafico, il rapporto incrementale Δs/Δt (ovvero tg θ) rappresenta la velocità scalare media. La pendenza della tangente geometrica nel punto t esprime invece la velocità scalare istantanea al tempo t.
L’accelerazione descrive la rapidità con cui varia il vettore velocità nel tempo:
- accelerazione media: è definita come il rapporto tra la variazione del vettore velocità
Δve il corrispondente intervallo di tempoΔt:amedia = Δv / Δt - accelerazione istantanea: è il valore limite a cui tende l’accelerazione media per
Δtche tende a zero, ovvero la derivata prima del vettore velocità rispetto al tempo:
a = dv / dt
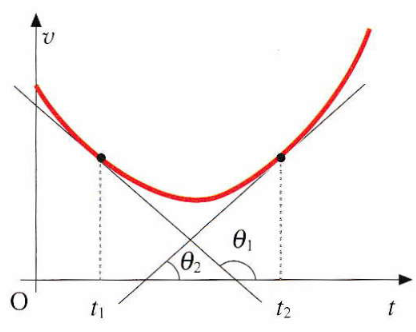
La pendenza della curva rappresenta la componente tangenziale dell’accelerazione, ovvero la variazione della velocità nella sua stessa direzione. Nel punto t1, l’accelerazione è negativa (la velocità diminuisce), mentre nel punto t2 è positiva (la velocità aumenta).
In un moto rettilineo, il vettore accelerazione è sempre parallelo alla traiettoria. Tuttavia, in un moto curvilineo, esso non è generalmente tangente. In questo caso, è fondamentale scomporre il vettore accelerazione in due componenti ortogonali:
- la componente tangenziale,
at, parallela al vettore velocità, che descrive la variazione del modulo della velocità. In un diagramma velocità-tempo, la pendenza della curva in un dato istante corrisponde precisamente al valore della componente tangenziale dell’accelerazione,at. - la componente normale,
an, perpendicolare al vettore velocità, che descrive la variazione della direzione della velocità, legata alla curvatura della traiettoria.
Nel Sistema Internazionale (S.I.), l’unità di misura della velocità è il metro al secondo (m s⁻¹), mentre quella dell’accelerazione è il metro al secondo quadrato (m s⁻²).
Definite queste grandezze fondamentali, è ora possibile procedere alla caratterizzazione analitica delle tipologie di moto più comuni incontrate nelle applicazioni ingegneristiche.
Tipologie di moto e loro leggi orarie
Questa sezione applica i concetti precedentemente esposti per analizzare alcuni modelli di moto di fondamentale importanza. Lo studio di moti semplici come quello rettilineo, circolare e armonico non è un mero esercizio teorico, ma fornisce i modelli di base essenziali per descrivere, analizzare e prevedere il comportamento cinematico di componenti e sistemi meccanici anche molto complessi.
Moto rettilineo uniforme
Un corpo si muove di moto rettilineo uniforme quando il suo vettore velocità v si mantiene costante in modulo, direzione e verso.
- Condizioni:
a = 0;v = costante. - Legge oraria: la traiettoria è una retta e la posizione
xvaria linearmente con il tempo, secondo la relazione:x = x₀ + v₀tdovex₀è la posizione all’istante inizialet=0ev₀è la velocità costante. Il grafico spazio-tempo di questo moto è una retta.
Moto rettilineo uniformemente accelerato
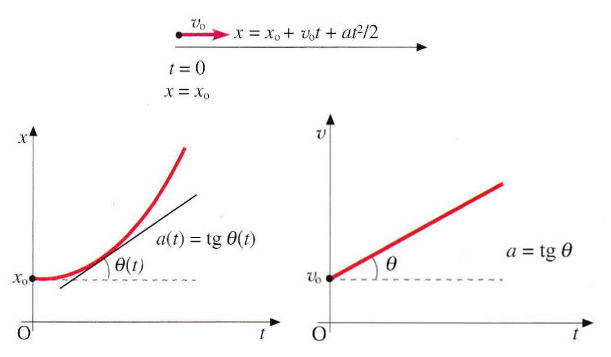
Questo moto descrive un corpo che si muove lungo una retta con un’accelerazione a costante in modulo, direzione e verso. L’accelerazione deve essere parallela alla velocità iniziale (o il corpo deve partire da fermo).
- equazione della velocità: la velocità varia linearmente nel tempo:
v = v₀ + at - legge oraria: la posizione varia secondo una funzione parabolica del tempo:
x = x₀ + v₀t + (1/2)at²
Esempio applicativo
Problema: un’automobile accelera da ferma (v₀=0) con un’accelerazione costante di a = 2.5 m s⁻². Calcolare il tempo necessario a raggiungere la velocità di 24 m s⁻¹ e lo spazio percorso in tale tempo.
Soluzione:
- calcolo del tempo: utilizzando la formula precedentemente descritta, si ricava
t = v/a= (24 m s⁻¹)/(2.5 m s⁻²)= 9.6 s - calcolo dello spazio: utilizzando l’altra formula con
x₀=0ev₀=0.x = (1/2)at² = 0.5 * (2.5 m s⁻²) * (9.6 s)² = 115.2 m
L’automobile impiega 9.6 secondi per raggiungere la velocità desiderata, percorrendo 115.2 metri.
Moto circolare uniforme
Il moto circolare uniforme descrive un punto che si muove lungo una circonferenza con velocità costante in modulo, ma non in direzione.
- Velocità angolare (
ω): è la rapidità con cui varia l’angoloθdescritto dal raggio vettore. Si definisce come:ω = Δθ / Δt - relazione tra velocità: la velocità periferica (tangenziale)
ve la velocità angolareωsono legate dal raggioRdella circonferenza:v = ωR - accelerazione: essendo il vettore velocità sempre tangente alla traiettoria, la sua direzione varia istante per istante. L’analisi differenziale del vettore velocità
vmostra che la variazione infinitesimadvè un vettore orientato radialmente verso il centro della circonferenza. Di conseguenza, il vettore accelerazionea = dv/dtè puramente normale (o centripeta), responsabile unicamente del cambiamento di direzione della velocità e non del suo modulo. Il suo modulo è dato da:a = v² / R = ω²R.
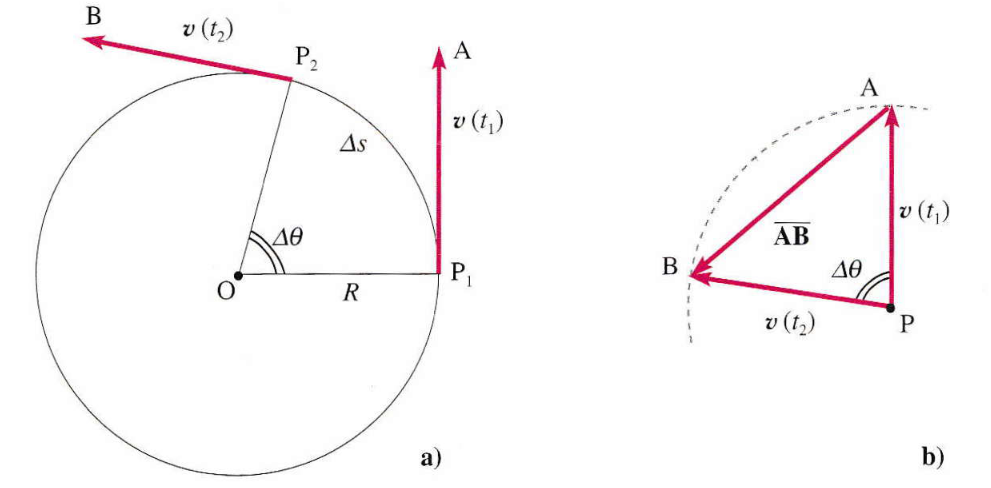
Moto circolare uniforme (a) La velocità è sempre tangente alla traiettoria e costante in modulo.
(b) L’accelerazione, ottenuta tramite costruzione geometrica, è diretta lungo il raggio dell’orbita e rivolta verso il centro: si tratta della accelerazione centripeta.
Esempio applicativo
Problema: calcolare l’accelerazione a cui sono sottoposte le particelle in una centrifuga con raggio di 15 cm (0.15 m) che opera a 20,000 rotazioni al minuto.
Soluzione:
- conversione della velocità angolare:
ω = 20,000 rot/min * (2π rad / 1 rot) * (1 min / 60 s) ≈ 2094.4 rad s⁻¹ - calcolo dell’accelerazione centripeta: utilizzando la formula:
a = ω²R = (2094.4 rad s⁻¹)² * 0.15 m ≈ 6.58 * 10⁵ m s⁻²
Il risultato mostra un’accelerazione di entità straordinaria, pari a circa 67.140 volte l’accelerazione di gravità (g ≈ 9.8 m s⁻²), evidenziando l’efficacia di tali dispositivi nella separazione di componenti basata sulla massa.
Caricamento….
Moto armonico
Il moto armonico è un moto periodico oscillatorio in cui la posizione del punto varia nel tempo secondo una legge sinusoidale.
- Legge oraria:
x = A sin(ωt + φ)doveAè l’ampiezza (massimo spostamento dal centro),ωè la pulsazione (legata alla frequenza) eφè la fase iniziale (che determina la posizione at=0) - velocità: derivando la legge oraria rispetto al tempo si ottiene:
v = dx/dt = Aω cos(ωt + φ) - accelerazione: derivando ulteriormente la velocità, si ottiene:
a = dv/dt = -Aω² sin(ωt + φ)
Sostituendo l’espressione di x nella formula dell’accelerazione, si giunge alla relazione fondamentale che caratterizza il moto armonico: a = -ω²x.
Questa equazione è di fondamentale importanza, in quanto rappresenta l’equazione differenziale che definisce il moto armonico. Essa stabilisce che ogni volta che un sistema è soggetto a un’accelerazione (e quindi, per la dinamica, a una forza) proporzionale e opposta allo spostamento, il moto risultante sarà inevitabilmente di tipo sinusoidale, come descritto dalla legge oraria.
Moto armonico: diagrammi spazio-tempo e velocità-tempo
La linea rossa continua rappresenta il diagramma spazio-tempo. La linea punteggiata mostra il diagramma velocità-tempo. Entrambi illustrano le oscillazioni caratteristiche del moto armonico.
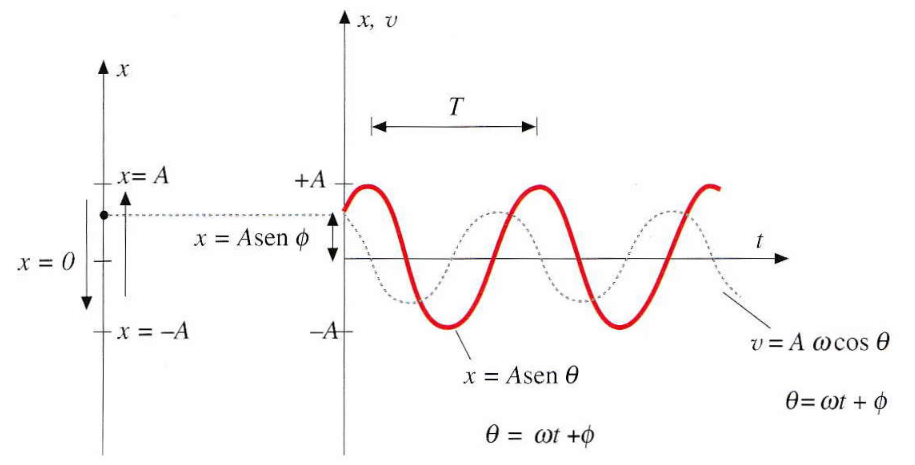
Fonte: Fisica biomedica.