Forze di trascinamento viscoso ad alta e bassa velocità (legge di Stokes)
Pubblicato da Raffo in Fisica
Le forze di trascinamento viscoso sono forze di attrito che, nel moto di un oggetto attraverso un fluido reale, si oppongono ad esso rallentandolo.
Esistono due regimi di velocità: a velocità molto bassa e a velocità alta.
Forze di trascinamento a bassa velocità
La forza di trascinamento a bassa velocità è dovuta alle forze di viscosità ed è proporzionale alla velocità: FR = -bv, dove b è il coefficiente di attrito viscoso.
Nel caso di oggetti sferici di raggio r, in regime laminare, b=-6πrη e quindi la FR è proporzionale a η (coefficiente di viscosità) e alle dimensioni dell’oggetto in moto ed è data dalla legge i Stokes: FR=-6πrηv.
Dalla legge di Stokes si può notare come la forza di trascinamento viscoso a bassa velocità non dipende dalla densità del liquido ρl. La legge di Stokes è valida solo se la velocità è molto bassa.
In termini del numero di Reynolds, un valore proporzionale al rapporto tra le forze d’inerzia e le forze viscose, per una sfera di raggio r, la legge di Stokes è valida se:
Se NR ≥ 1, la FR diventa proporzionale a v2, a condizione che la v sia ancora in regime laminare e non turbolento.
Per oggetti che possiedono forme diverse, la legge di Stokes è ancora valida, ma il coefficiente NR va determinato sperimentalmente ed r è visto come una dimensione caratteristica dell’oggetto.
Quando si parla di forze di trascinamento viscoso, molto importante è introdurre il coefficiente di mobilità μ che corrisponde al rapporto tra la velocità limite di trascinamento vl e la forza di attrito viscoso FR:
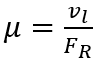
L’unità di misura del coefficiente di mobilità è il s/Kg.
Esso dipende dalle proprietà del mezzo viscoso e dalle caratteristiche della particella in moto nel mezzo viscoso, infatti, essendo FR = -bv, considerando v= vl:
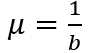
Sedimentazione
Considerando una particella sferica di raggio r e densità ρ in caduta libera in un fluido di viscosità η e densità ρl, per determinare la velocità limite, di trascinamento o di sedimentazione vl bisogna ragionare in senso di equilibrio di forze. Infatti la vl è raggiunta quando la forza di attrito viscoso FR e la spinta di archimede FA eguagliano la forza peso FP (FR+FA+FP=0 ovvero FR+FA=-FP). Andando a sostituire le rispettive forze, avremo:
6πrηvl + FA = mg.
La spinta di Archimede FA verso l’alto è pari al peso di fluido spostato: FA = ρlgV. Trattandosi di una particella sferica, il volume è V= (4/3)πr3.
Inoltre, considerando la forza peso FP=ρVg, quando si raggiunge l’equilibrio dinamico:
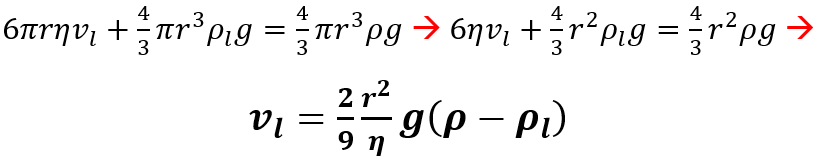
Dall’equazione ottenuta si può notare che misurando la velocità di sedimentazione vl e il raggio r delle particelle, si può determinare la viscosità η del fluido. Infatti vl dipende dalle dimensioni e dalla densità della particella, ma anche dal coefficiente di viscosità e la densità del fluido dove è immersa.
Mediante sedimentazione, si possono separare particelle diverse presenti in una sospensione in base alle loro dimensioni e densità.
Quando la velocità di sedimentazione è molto lenta, si usano tecniche che permettono di accelerarla come la centrifugazione.
Forze di trascinamento ad alta velocità
Quando la v di un corpo che si muove in un fluido viscoso cresce in modo tale che NR ≥ 1 la FR di attrito viscoso o trascinamento opposta dal fluido diventa proporzionale a v2. Quindi:
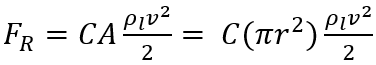
Dove A = π R2 è la sezione della particella intesa come sfera e ρl v2/2 è l’energia cinetica dell’unità di volume del fluido con densità ρl. C è un coefficiente adimensionale che dipende dalla forma geometrica del corpo e viene determinato sperimentalmente.
Nel caso delle forze di trascinamento viscoso ad alta velocità manca la dipendenza da η. Ciò è in accordo con l’idea che la FR nasce solo quando NR ≥ 1, ovvero dall’accelerazione del fluido che si muove intorno alla sfera e non da effetti di viscosità.
La relazione di FR ad alta velocità è valida per oggetti di qualsiasi forma, dove A è la sezione trasversale dell’oggetto perpendicolare alla direzione del moto. Ciò avviene nonostante il moto del fluido intorno al cilindro varia da laminare a turbolento per NR = 100.
